Alexandru C. Serban
Counterexample-Guided Strategy Improvement for POMDPs Using Recurrent Neural Networks
Mar 21, 2019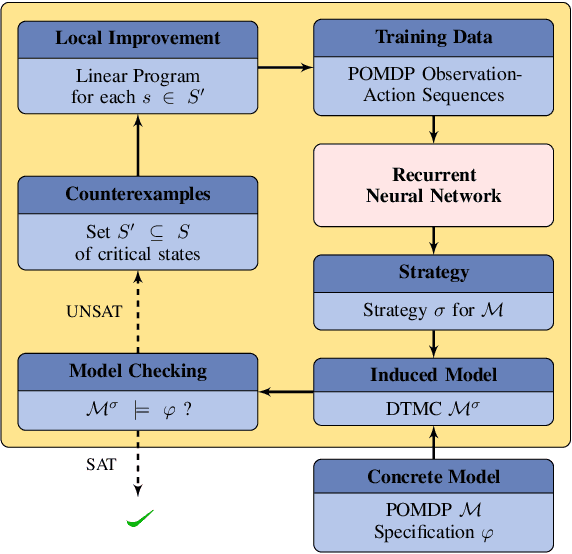
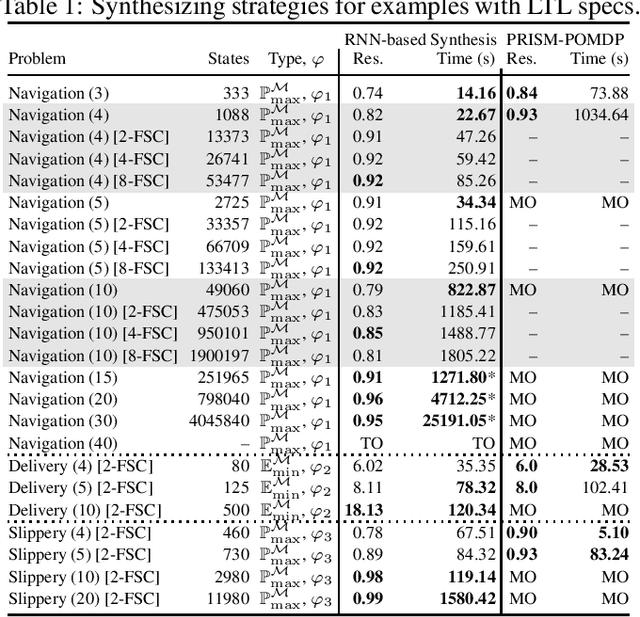
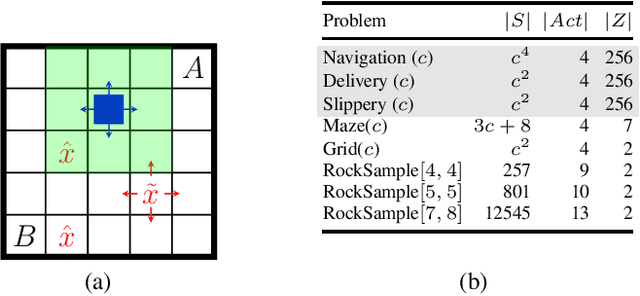
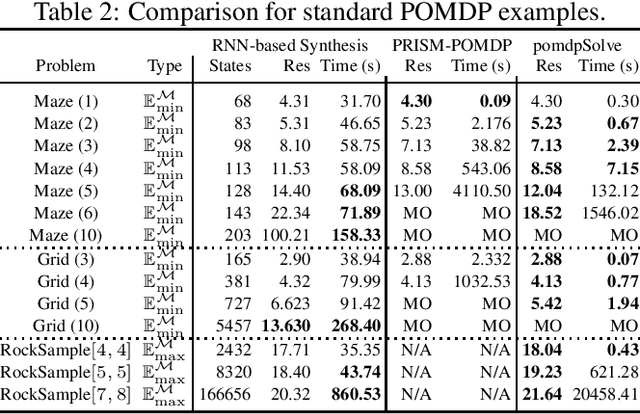
Abstract:We study strategy synthesis for partially observable Markov decision processes (POMDPs). The particular problem is to determine strategies that provably adhere to (probabilistic) temporal logic constraints. This problem is computationally intractable and theoretically hard. We propose a novel method that combines techniques from machine learning and formal verification. First, we train a recurrent neural network (RNN) to encode POMDP strategies. The RNN accounts for memory-based decisions without the need to expand the full belief space of a POMDP. Secondly, we restrict the RNN-based strategy to represent a finite-memory strategy and implement it on a specific POMDP. For the resulting finite Markov chain, efficient formal verification techniques provide provable guarantees against temporal logic specifications. If the specification is not satisfied, counterexamples supply diagnostic information. We use this information to improve the strategy by iteratively training the RNN. Numerical experiments show that the proposed method elevates the state of the art in POMDP solving by up to three orders of magnitude in terms of solving times and model sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge