Alexandra Schofield
More Than Words: Collocation Tokenization for Latent Dirichlet Allocation Models
Aug 24, 2021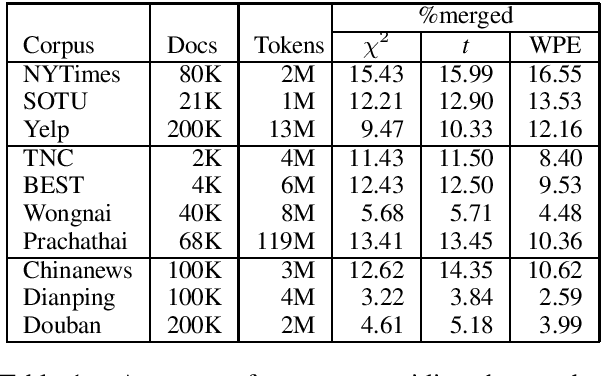


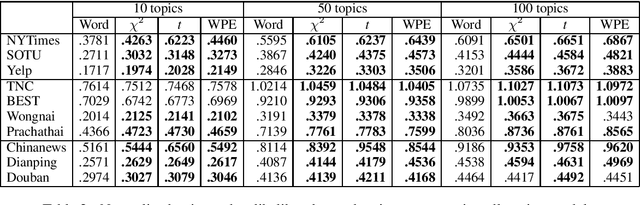
Abstract:Traditionally, Latent Dirichlet Allocation (LDA) ingests words in a collection of documents to discover their latent topics using word-document co-occurrences. However, it is unclear how to achieve the best results for languages without marked word boundaries such as Chinese and Thai. Here, we explore the use of Pearson's chi-squared test, t-statistics, and Word Pair Encoding (WPE) to produce tokens as input to the LDA model. The Chi-squared, t, and WPE tokenizers are trained on Wikipedia text to look for words that should be grouped together, such as compound nouns, proper nouns, and complex event verbs. We propose a new metric for measuring the clustering quality in settings where the vocabularies of the models differ. Based on this metric and other established metrics, we show that topics trained with merged tokens result in topic keys that are clearer, more coherent, and more effective at distinguishing topics than those unmerged models.
Locally Private Bayesian Inference for Count Models
Nov 05, 2018



Abstract:As more aspects of social interaction are digitally recorded, there is a growing need to develop privacy-preserving data analysis methods. Social scientists will be more likely to adopt these methods if doing so entails minimal change to their current methodology. Toward that end, we present a general and modular method for privatizing Bayesian inference for Poisson factorization, a broad class of models that contains some of the most widely used models in the social sciences. Our method satisfies local differential privacy, which ensures that no single centralized server need ever store the non-privatized data. To formulate our local-privacy guarantees, we introduce and focus on limited-precision local privacy---the local privacy analog of limited-precision differential privacy (Flood et al., 2013). We present two case studies, one involving social networks and one involving text corpora, that test our method's ability to form the posterior distribution over latent variables under different levels of noise, and demonstrate our method's utility over a na\"{i}ve approach, wherein inference proceeds as usual, treating the privatized data as if it were not privatized.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge