Clustering of graph vertex subset via Krylov subspace model reduction

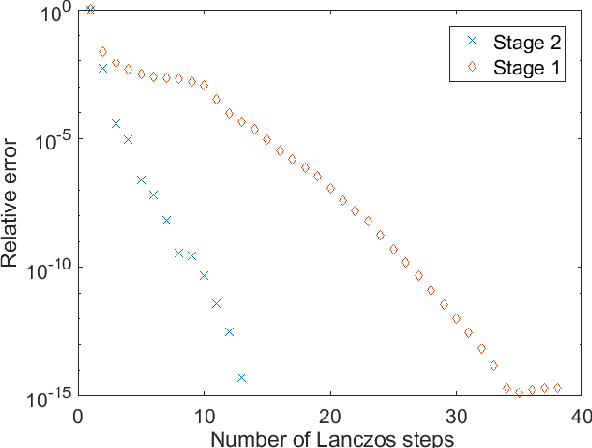
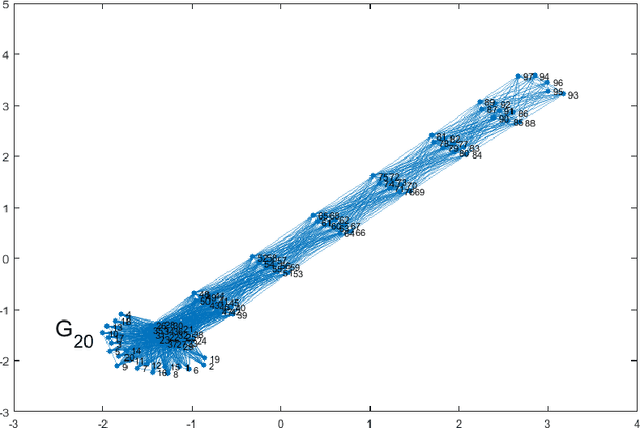
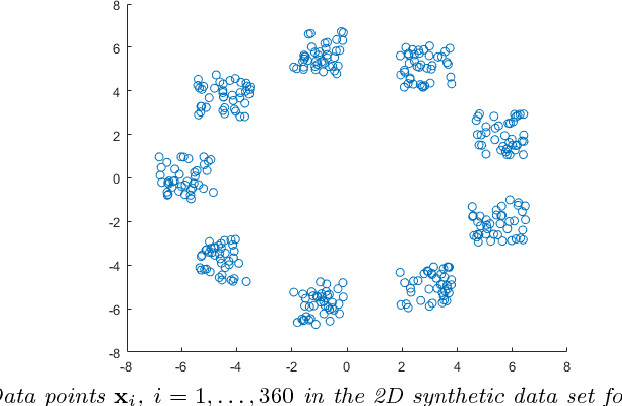
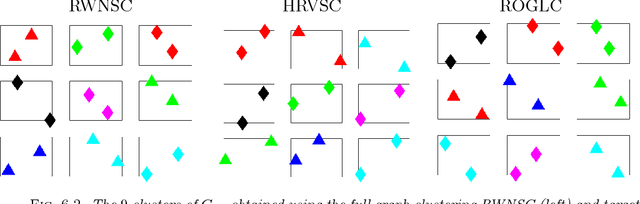
Clustering via graph-Laplacian spectral imbedding is ubiquitous in data science and machine learning. However, it becomes less efficient for large data sets due to two factors. First, computing the partial eigendecomposition of the graph-Laplacian typically requires a large Krylov subspace. Second, after the spectral imbedding is complete, the clustering is typically performed with various relaxations of k-means, which may become prone to getting stuck in local minima and scale poorly in terms of computational cost for large data sets. Here we propose two novel algorithms for spectral clustering of a subset of the graph vertices (target subset) based on the theory of model order reduction. They rely on realizations of a reduced order model (ROM) that accurately approximates the diffusion transfer function of the original graph for inputs and outputs restricted to the target subset. While our focus is limited to this subset, our algorithms produce its clustering that is consistent with the overall structure of the graph. Moreover, working with a small target subset reduces greatly the required dimension of Krylov subspace and allows to exploit the approximations of k-means in the regimes when they are most robust and efficient, as verified by the numerical experiments. There are several uses for our algorithms. First, they can be employed on their own to clusterize a representative subset in cases when the full graph clustering is either infeasible or not required. Second, they may be used for quality control. Third, as they drastically reduce the problem size, they enable the application of more powerful approximations of k-means like those based on semi-definite programming (SDP) instead of the conventional Lloyd's algorithm. Finally, they can be used as building blocks of a divide-and-conquer algorithm for the full graph clustering. The latter will be reported in a separate article.

Automated polyp detection in colon capsule endoscopy

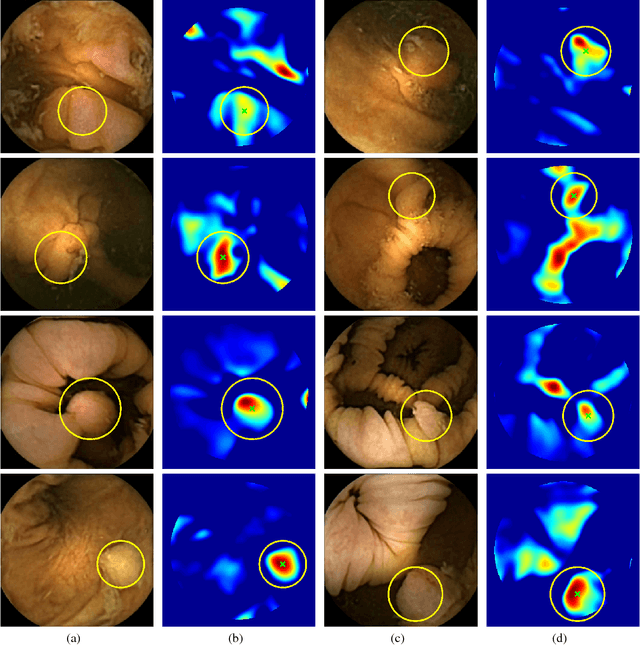
Colorectal polyps are important precursors to colon cancer, a major health problem. Colon capsule endoscopy (CCE) is a safe and minimally invasive examination procedure, in which the images of the intestine are obtained via digital cameras on board of a small capsule ingested by a patient. The video sequence is then analyzed for the presence of polyps. We propose an algorithm that relieves the labor of a human operator analyzing the frames in the video sequence. The algorithm acts as a binary classifier, which labels the frame as either containing polyps or not, based on the geometrical analysis and the texture content of the frame. The geometrical analysis is based on a segmentation of an image with the help of a mid-pass filter. The features extracted by the segmentation procedure are classified according to an assumption that the polyps are characterized as protrusions that are mostly round in shape. Thus, we use a best fit ball radius as a decision parameter of a binary classifier. We present a statistical study of the performance of our approach on a data set containing over 18,900 frames from the endoscopic video sequences of five adult patients. The algorithm demonstrates a solid performance, achieving 47% sensitivity per frame and over 81% sensitivity per polyp at a specificity level of 90%. On average, with a video sequence length of 3747 frames, only 367 false positive frames need to be inspected by a human operator.