Clustering of graph vertex subset via Krylov subspace model reduction
Paper and Code
Sep 09, 2018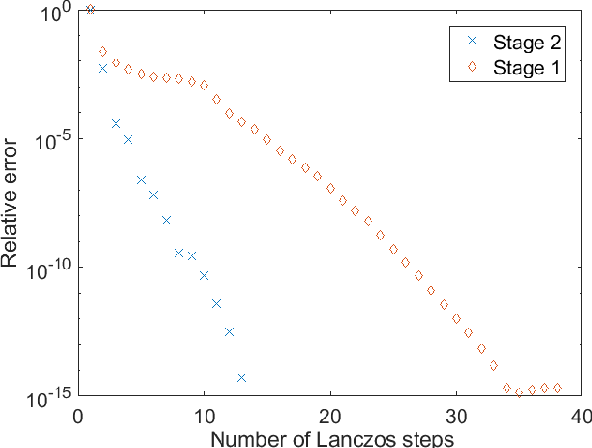
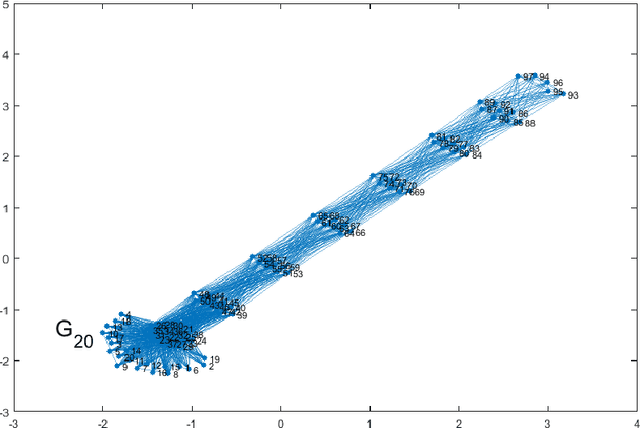
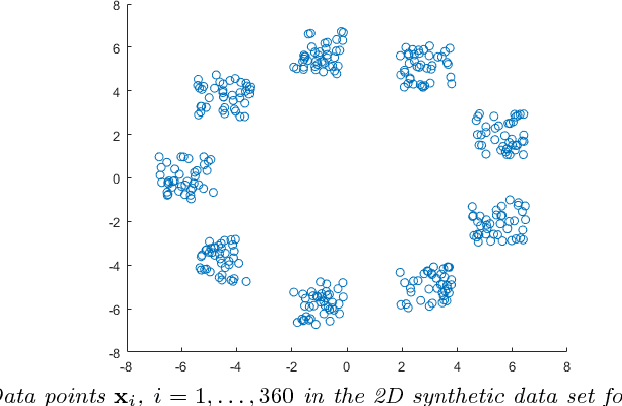
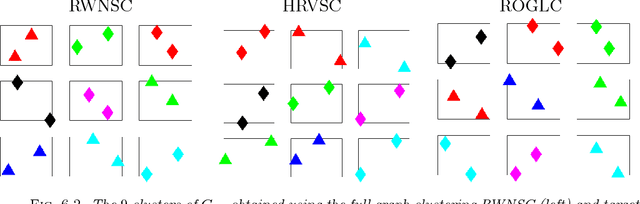
Clustering via graph-Laplacian spectral imbedding is ubiquitous in data science and machine learning. However, it becomes less efficient for large data sets due to two factors. First, computing the partial eigendecomposition of the graph-Laplacian typically requires a large Krylov subspace. Second, after the spectral imbedding is complete, the clustering is typically performed with various relaxations of k-means, which may become prone to getting stuck in local minima and scale poorly in terms of computational cost for large data sets. Here we propose two novel algorithms for spectral clustering of a subset of the graph vertices (target subset) based on the theory of model order reduction. They rely on realizations of a reduced order model (ROM) that accurately approximates the diffusion transfer function of the original graph for inputs and outputs restricted to the target subset. While our focus is limited to this subset, our algorithms produce its clustering that is consistent with the overall structure of the graph. Moreover, working with a small target subset reduces greatly the required dimension of Krylov subspace and allows to exploit the approximations of k-means in the regimes when they are most robust and efficient, as verified by the numerical experiments. There are several uses for our algorithms. First, they can be employed on their own to clusterize a representative subset in cases when the full graph clustering is either infeasible or not required. Second, they may be used for quality control. Third, as they drastically reduce the problem size, they enable the application of more powerful approximations of k-means like those based on semi-definite programming (SDP) instead of the conventional Lloyd's algorithm. Finally, they can be used as building blocks of a divide-and-conquer algorithm for the full graph clustering. The latter will be reported in a separate article.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge