Distributed Saddle-Point Problems Under Similarity

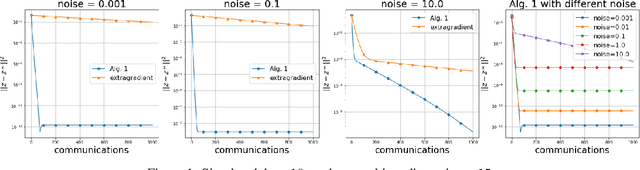
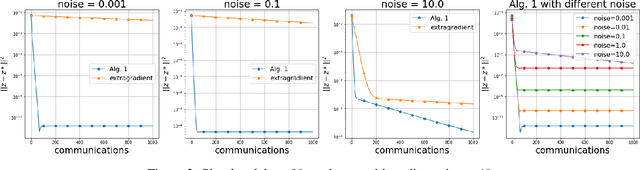
We study solution methods for (strongly-)convex-(strongly)-concave Saddle-Point Problems (SPPs) over networks of two type - master/workers (thus centralized) architectures and meshed (thus decentralized) networks. The local functions at each node are assumed to be similar, due to statistical data similarity or otherwise. We establish lower complexity bounds for a fairly general class of algorithms solving the SPP. We show that a given suboptimality $\epsilon>0$ is achieved over master/workers networks in $\Omega\big(\Delta\cdot \delta/\mu\cdot \log (1/\varepsilon)\big)$ rounds of communications, where $\delta>0$ measures the degree of similarity of the local functions, $\mu$ is their strong convexity constant, and $\Delta$ is the diameter of the network. The lower communication complexity bound over meshed networks reads $\Omega\big(1/{\sqrt{\rho}} \cdot {\delta}/{\mu}\cdot\log (1/\varepsilon)\big)$, where $\rho$ is the (normalized) eigengap of the gossip matrix used for the communication between neighbouring nodes. We then propose algorithms matching the lower bounds over either types of networks (up to log-factors). We assess the effectiveness of the proposed algorithms on a robust logistic regression problem.

ADOM: Accelerated Decentralized Optimization Method for Time-Varying Networks

We propose ADOM - an accelerated method for smooth and strongly convex decentralized optimization over time-varying networks. ADOM uses a dual oracle, i.e., we assume access to the gradient of the Fenchel conjugate of the individual loss functions. Up to a constant factor, which depends on the network structure only, its communication complexity is the same as that of accelerated Nesterov gradient method (Nesterov, 2003). To the best of our knowledge, only the algorithm of Rogozin et al. (2019) has a convergence rate with similar properties. However, their algorithm converges under the very restrictive assumption that the number of network changes can not be greater than a tiny percentage of the number of iterations. This assumption is hard to satisfy in practice, as the network topology changes usually can not be controlled. In contrast, ADOM merely requires the network to stay connected throughout time.