Topological Analysis of Syntactic Structures

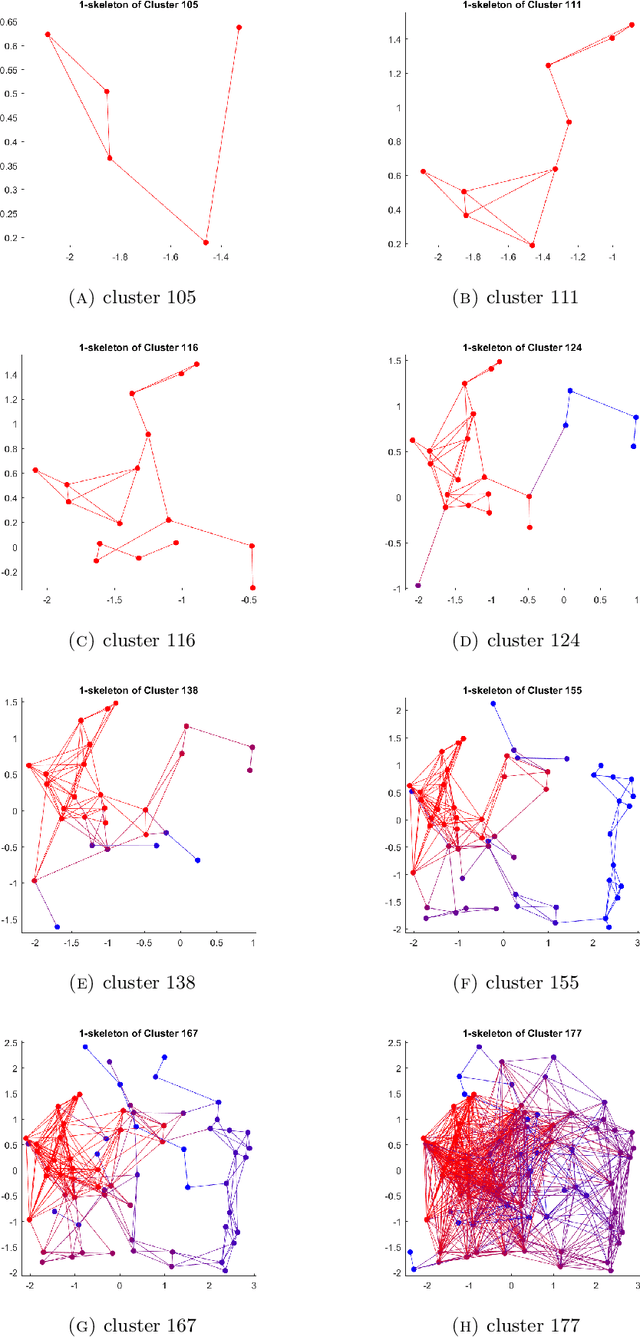
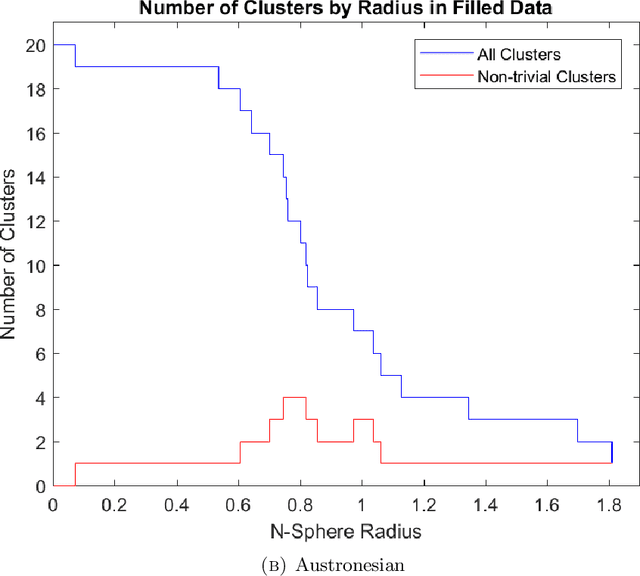
We use the persistent homology method of topological data analysis and dimensional analysis techniques to study data of syntactic structures of world languages. We analyze relations between syntactic parameters in terms of dimensionality, of hierarchical clustering structures, and of non-trivial loops. We show there are relations that hold across language families and additional relations that are family-specific. We then analyze the trees describing the merging structure of persistent connected components for languages in different language families and we show that they partly correlate to historical phylogenetic trees but with significant differences. We also show the existence of interesting non-trivial persistent first homology groups in various language families. We give examples where explicit generators for the persistent first homology can be identified, some of which appear to correspond to homoplasy phenomena, while others may have an explanation in terms of historical linguistics, corresponding to known cases of syntactic borrowing across different language subfamilies.

Persistent Topology of Syntax

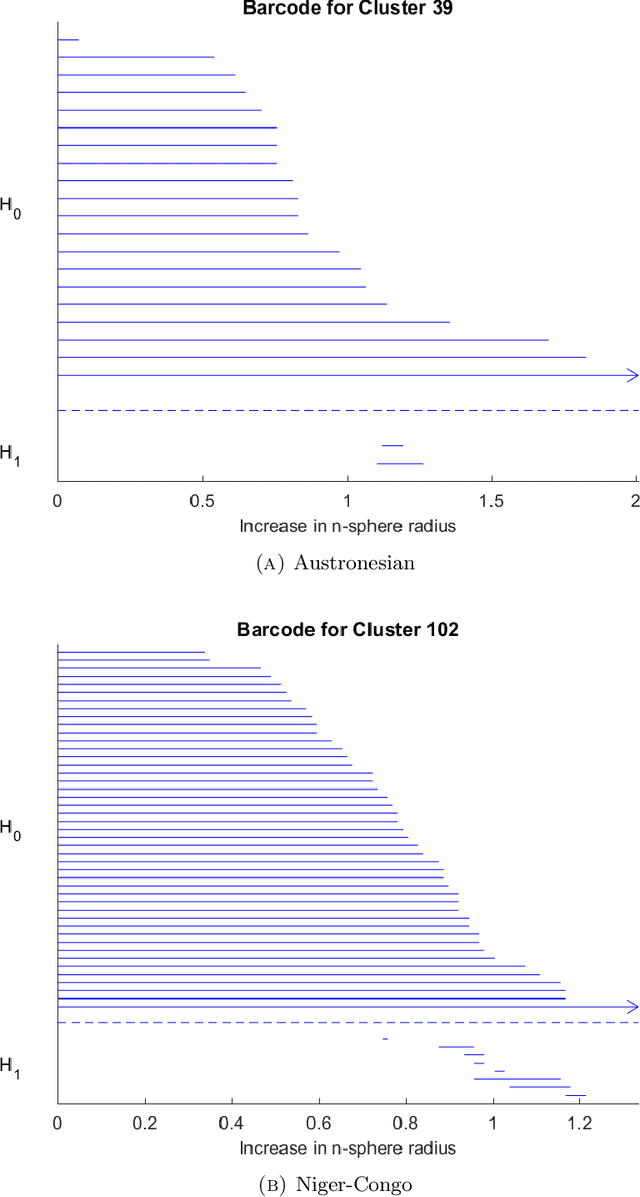
We study the persistent homology of the data set of syntactic parameters of the world languages. We show that, while homology generators behave erratically over the whole data set, non-trivial persistent homology appears when one restricts to specific language families. Different families exhibit different persistent homology. We focus on the cases of the Indo-European and the Niger-Congo families, for which we compare persistent homology over different cluster filtering values. We investigate the possible significance, in historical linguistic terms, of the presence of persistent generators of the first homology. In particular, we show that the persistent first homology generator we find in the Indo-European family is not due (as one might guess) to the Anglo-Norman bridge in the Indo-European phylogenetic network, but is related to the position of Ancient Greek and the Hellenic branch within the network.