Topological Analysis of Syntactic Structures
Paper and Code
Mar 12, 2019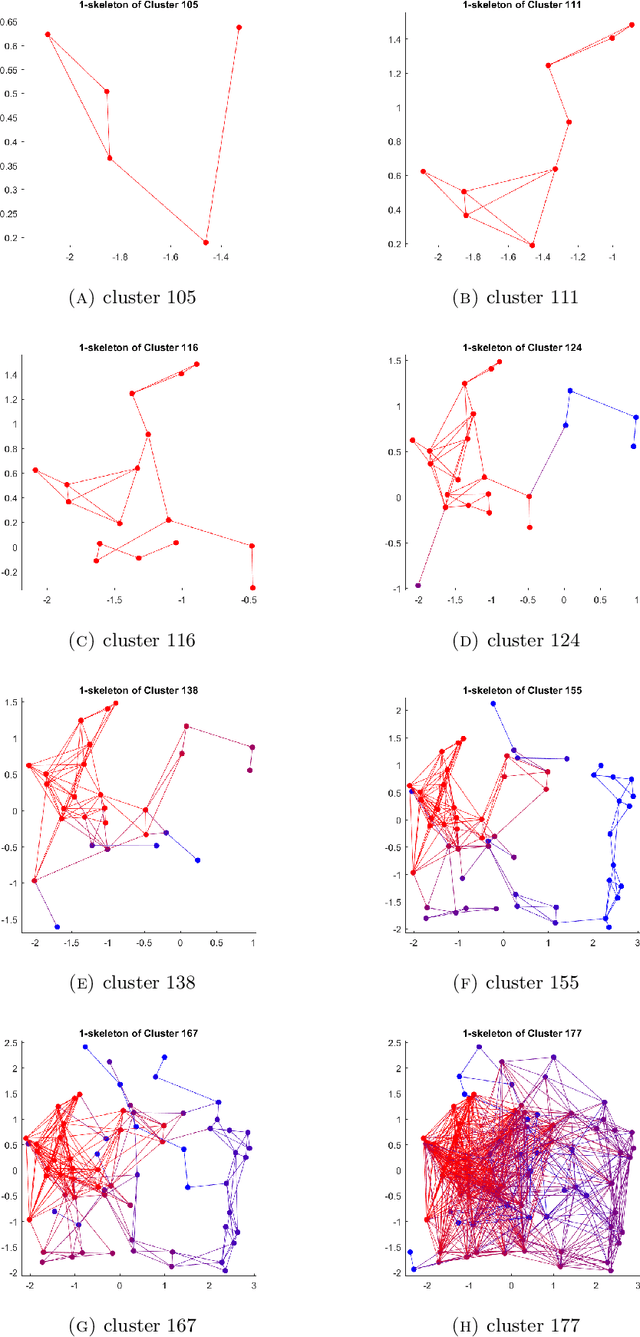
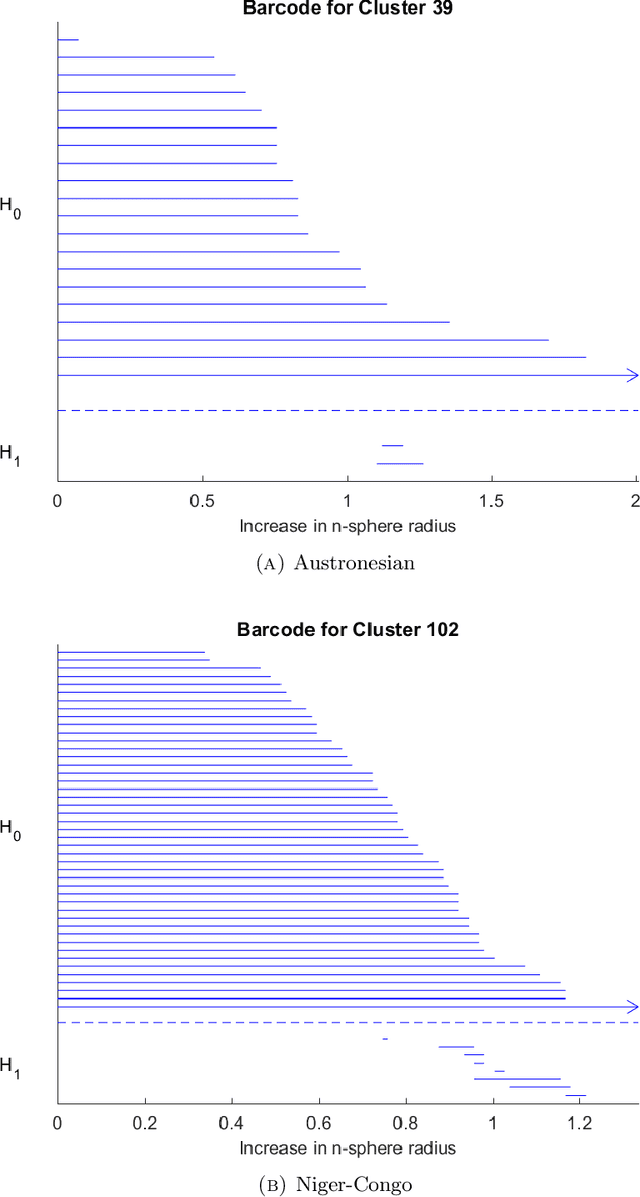
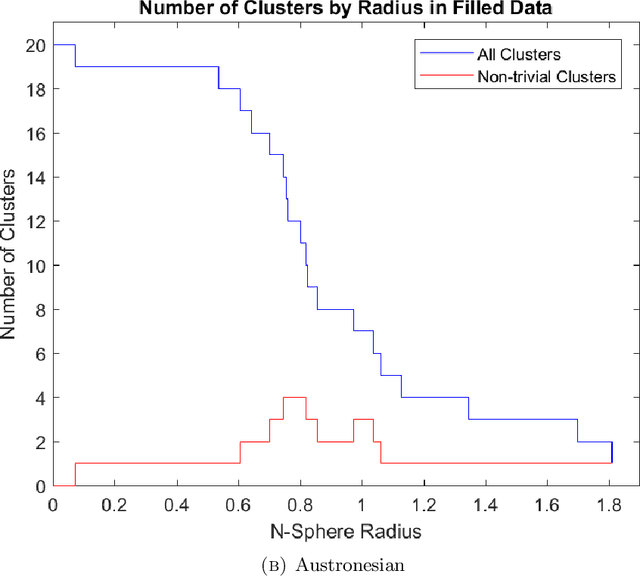
We use the persistent homology method of topological data analysis and dimensional analysis techniques to study data of syntactic structures of world languages. We analyze relations between syntactic parameters in terms of dimensionality, of hierarchical clustering structures, and of non-trivial loops. We show there are relations that hold across language families and additional relations that are family-specific. We then analyze the trees describing the merging structure of persistent connected components for languages in different language families and we show that they partly correlate to historical phylogenetic trees but with significant differences. We also show the existence of interesting non-trivial persistent first homology groups in various language families. We give examples where explicit generators for the persistent first homology can be identified, some of which appear to correspond to homoplasy phenomena, while others may have an explanation in terms of historical linguistics, corresponding to known cases of syntactic borrowing across different language subfamilies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge