Noisy Group Testing with Side Information

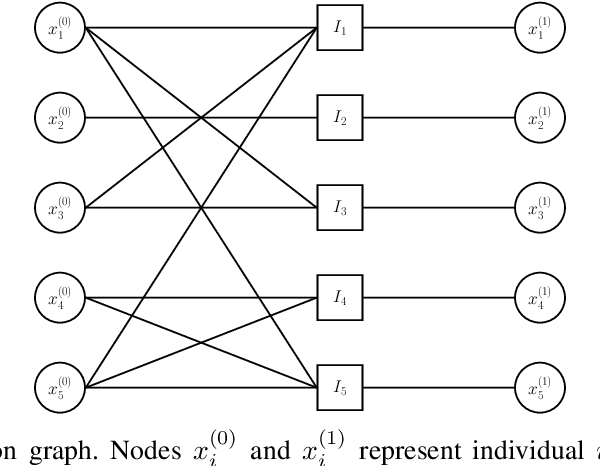
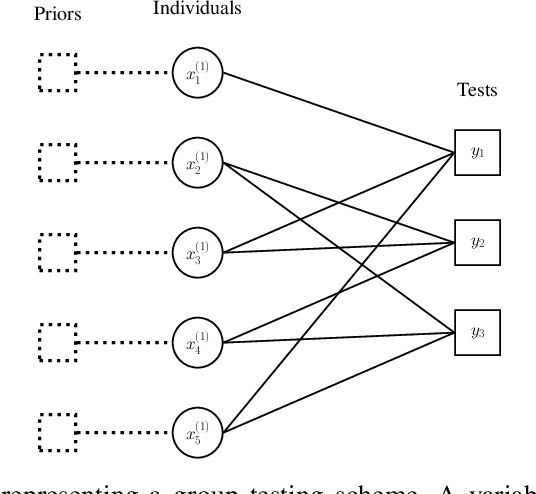
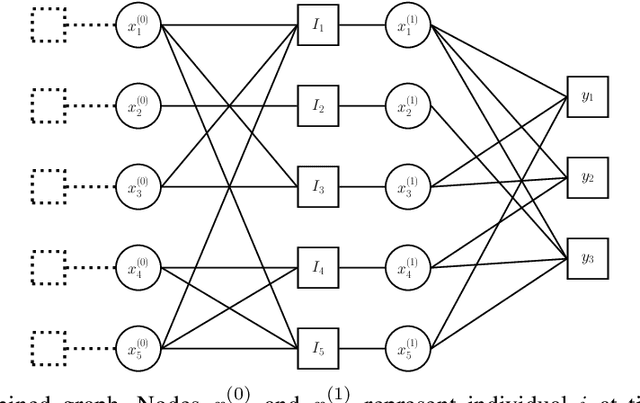
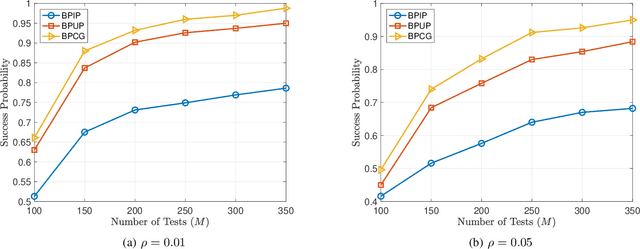
Group testing has recently attracted significant attention from the research community due to its applications in diagnostic virology. An instance of the group testing problem includes a ground set of individuals which includes a small subset of infected individuals. The group testing procedure consists of a number of tests, such that each test indicates whether or not a given subset of individuals includes one or more infected individuals. The goal of the group testing procedure is to identify the subset of infected individuals with the minimum number of tests. Motivated by practical scenarios, such as testing for viral diseases, this paper focuses on the following group testing settings: (i) the group testing procedure is noisy, i.e., the outcome of the group testing procedure can be flipped with a certain probability; (ii) there is a certain amount of side information on the distribution of the infected individuals available to the group testing algorithm. The paper makes the following contributions. First, we propose a probabilistic model, referred to as an interaction model, that captures the side information about the probability distribution of the infected individuals. Next, we present a decoding scheme, based on the belief propagation, that leverages the interaction model to improve the decoding accuracy. Our results indicate that the proposed algorithm achieves higher success probability and lower false-negative and false-positive rates when compared to the traditional belief propagation especially in the high noise regime.

The Linear Capacity of Single-Server Individually-Private Information Retrieval with Side Information

This paper considers the problem of single-server Individually-Private Information Retrieval with side information (IPIR). In this problem, there is a remote server that stores a dataset of $K$ messages, and there is a user that initially knows $M$ of these messages, and wants to retrieve $D$ other messages belonging to the dataset. The goal of the user is to retrieve the $D$ desired messages by downloading the minimum amount of information from the server while revealing no information about whether an individual message is one of the $D$ desired messages. In this work, we focus on linear IPIR schemes, i.e., the IPIR schemes in which the user downloads only linear combinations of the original messages from the server. We prove a converse bound on the download rate of any linear IPIR scheme for all $K,D,M$, and show the achievability of this bound for all $K,D,M$ satisfying a certain divisibility condition. Our results characterize the linear capacity of IPIR, which is defined as the maximum achievable download rate over all linear IPIR schemes, for a wide range of values of $K,D,M$.

The Role of Reusable and Single-Use Side Information in Private Information Retrieval

This paper introduces the problem of Private Information Retrieval with Reusable and Single-use Side Information (PIR-RSSI). In this problem, one or more remote servers store identical copies of a set of $K$ messages, and there is a user that initially knows $M$ of these messages, and wants to privately retrieve one other message from the set of $K$ messages. The objective is to design a retrieval scheme in which the user downloads the minimum amount of information from the server(s) while the identity of the message wanted by the user and the identities of an $M_1$-subset of the $M$ messages known by the user (referred to as reusable side information) are protected, but the identities of the remaining $M_2=M-M_1$ messages known by the user (referred to as single-use side information) do not need to be protected. The PIR-RSSI problem reduces to the classical Private Information Retrieval (PIR) problem when ${M_1=M_2=0}$, and reduces to the problem of PIR with Private Side Information or PIR with Side Information when ${M_1\geq 1,M_2=0}$ or ${M_1=0,M_2\geq 1}$, respectively. In this work, we focus on the single-server setting of the PIR-RSSI problem. We characterize the capacity of this setting for the cases of ${M_1=1,M_2\geq 1}$ and ${M_1\geq 1,M_2=1}$, where the capacity is defined as the maximum achievable download rate over all PIR-RSSI schemes. Our results show that for sufficiently small values of $K$, the single-use side information messages can help in reducing the download cost only if they are kept private; and for larger values of $K$, the reusable side information messages cannot help in reducing the download cost.

Multi-Server Private Linear Transformation with Joint Privacy

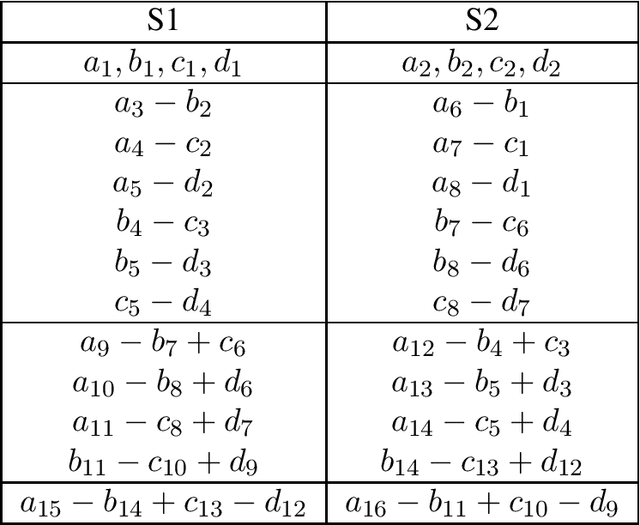
This paper focuses on the Private Linear Transformation (PLT) problem in the multi-server scenario. In this problem, there are $N$ servers, each of which stores an identical copy of a database consisting of $K$ independent messages, and there is a user who wishes to compute $L$ independent linear combinations of a subset of $D$ messages in the database while leaking no information to the servers about the identity of the entire set of these $D$ messages required for the computation. We focus on the setting in which the coefficient matrix of the desired $L$ linear combinations generates a Maximum Distance Separable (MDS) code. We characterize the capacity of the PLT problem, defined as the supremum of all achievable download rates, for all parameters $N, K, D \geq 1$ and $L=1$, i.e., when the user wishes to compute one linear combination of $D$ messages. Moreover, we establish an upper bound on the capacity of PLT problem for all parameters $N, K, D, L \geq 1$, and leveraging some known capacity results, we show the tightness of this bound in the following regimes: (i) the case when there is a single server (i.e., $N=1$), (ii) the case when $L=1$, and (iii) the case when $L=D$.

Single-Server Private Linear Transformation: The Individual Privacy Case

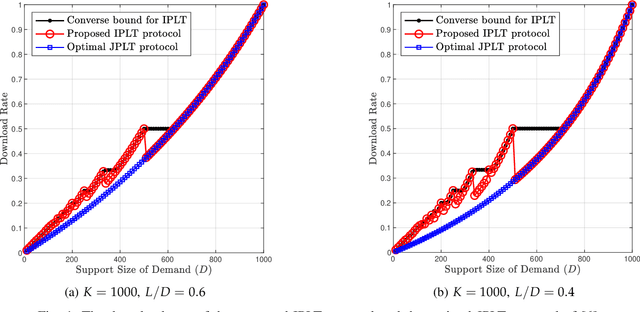
This paper considers the single-server Private Linear Transformation (PLT) problem with individual privacy guarantees. In this problem, there is a user that wishes to obtain $L$ independent linear combinations of a $D$-subset of messages belonging to a dataset of $K$ messages stored on a single server. The goal is to minimize the download cost while keeping the identity of each message required for the computation individually private. The individual privacy requirement ensures that the identity of each individual message required for the computation is kept private. This is in contrast to the stricter notion of joint privacy that protects the entire set of identities of all messages used for the computation, including the correlations between these identities. The notion of individual privacy captures a broad set of practical applications. For example, such notion is relevant when the dataset contains information about individuals, each of them requires privacy guarantees for their data access patterns. We focus on the setting in which the required linear transformation is associated with a maximum distance separable (MDS) matrix. In particular, we require that the matrix of coefficients pertaining to the required linear combinations is the generator matrix of an MDS code. We establish lower and upper bounds on the capacity of PLT with individual privacy, where the capacity is defined as the supremum of all achievable download rates. We show that our bounds are tight under certain conditions.

Single-Server Private Linear Transformation: The Joint Privacy Case

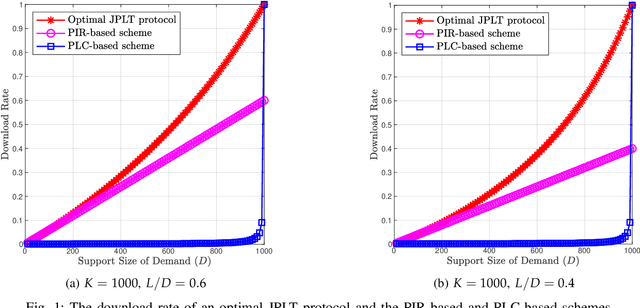
This paper introduces the problem of Private Linear Transformation (PLT) which generalizes the problems of private information retrieval and private linear computation. The PLT problem includes one or more remote server(s) storing (identical copies of) $K$ messages and a user who wants to compute $L$ independent linear combinations of a $D$-subset of messages. The objective of the user is to perform the computation by downloading minimum possible amount of information from the server(s), while protecting the identities of the $D$ messages required for the computation. In this work, we focus on the single-server setting of the PLT problem when the identities of the $D$ messages required for the computation must be protected jointly. We consider two different models, depending on whether the coefficient matrix of the required $L$ linear combinations generates a Maximum Distance Separable (MDS) code. We prove that the capacity for both models is given by $L/(K-D+L)$, where the capacity is defined as the supremum of all achievable download rates. Our converse proofs are based on linear-algebraic and information-theoretic arguments that establish connections between PLT schemes and linear codes. We also present an achievability scheme for each of the models being considered.

Private Linear Transformation: The Individual Privacy Case

This paper considers the single-server Private Linear Transformation (PLT) problem when individual privacy is required. In this problem, there is a user that wishes to obtain $L$ linear combinations of a $D$-subset of messages belonging to a dataset of $K$ messages stored on a single server. The goal is to minimize the download cost while keeping the identity of every message required for the computation individually private. The individual privacy requirement implies that, from the perspective of the server, every message is equally likely to belong to the $D$-subset of messages that constitute the support set of the required linear combinations. We focus on the setting in which the matrix of coefficients pertaining to the required linear combinations is the generator matrix of a Maximum Distance Separable code. We establish lower and upper bounds on the capacity of PLT with individual privacy, where the capacity is defined as the supremum of all achievable download rates. We show that our bounds are tight under certain divisibility conditions. In addition, we present lower bounds on the capacity of the settings in which the user has a prior side information about a subset of messages.

Private Linear Transformation: The Joint Privacy Case

We introduce the problem of Private Linear Transformation (PLT). This problem includes a single (or multiple) remote server(s) storing (identical copies of) $K$ messages and a user who wants to compute $L$ linear combinations of a $D$-subset of these messages by downloading the minimum amount of information from the server(s) while protecting the privacy of the entire set of $D$ messages. This problem generalizes the Private Information Retrieval and Private Linear Computation problems. In this work, we focus on the single-server case. For the setting in which the coefficient matrix of the required $L$ linear combinations generates a Maximum Distance Separable (MDS) code, we characterize the capacity -- defined as the supremum of all achievable download rates, for all parameters $K, D, L$. In addition, we present lower and/or upper bounds on the capacity for the settings with non-MDS coefficient matrices and the settings with a prior side information.