Multi-Server Private Linear Computation with Joint and Individual Privacy Guarantees

This paper considers the problem of multi-server Private Linear Computation, under the joint and individual privacy guarantees. In this problem, identical copies of a dataset comprised of $K$ messages are stored on $N$ non-colluding servers, and a user wishes to obtain one linear combination of a $D$-subset of messages belonging to the dataset. The goal is to design a scheme for performing the computation such that the total amount of information downloaded from the servers is minimized, while the privacy of the $D$ messages required for the computation is protected. When joint privacy is required, the identities of all of these $D$ messages must be kept private jointly, and when individual privacy is required, the identity of every one of these $D$ messages must be kept private individually. In this work, we characterize the capacity, which is defined as the maximum achievable download rate, under both joint and individual privacy requirements. In particular, we show that when joint privacy is required the capacity is given by ${(1+1/N+\dots+1/N^{K-D})^{-1}}$, and when individual privacy is required the capacity is given by ${(1+1/N+\dots+1/N^{\lceil K/D\rceil-1})^{-1}}$ assuming that $D$ divides $K$, or $K\pmod D$ divides $D$. Our converse proofs are based on reduction from two variants of the multi-server Private Information Retrieval problem in the presence of side information. Our achievability schemes build up on our recently proposed schemes for single-server Private Linear Transformation and the multi-server private computation scheme proposed by Sun and Jafar. Using similar proof techniques, we also establish upper and lower bounds on the capacity for the cases in which the user wants to compute $L$ (potentially more than one) linear combinations.

Single-Server Private Linear Transformation: The Individual Privacy Case

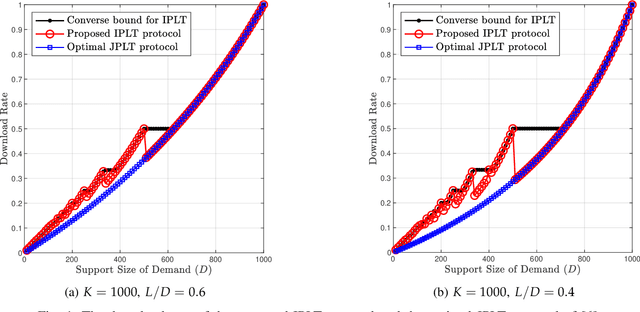
This paper considers the single-server Private Linear Transformation (PLT) problem with individual privacy guarantees. In this problem, there is a user that wishes to obtain $L$ independent linear combinations of a $D$-subset of messages belonging to a dataset of $K$ messages stored on a single server. The goal is to minimize the download cost while keeping the identity of each message required for the computation individually private. The individual privacy requirement ensures that the identity of each individual message required for the computation is kept private. This is in contrast to the stricter notion of joint privacy that protects the entire set of identities of all messages used for the computation, including the correlations between these identities. The notion of individual privacy captures a broad set of practical applications. For example, such notion is relevant when the dataset contains information about individuals, each of them requires privacy guarantees for their data access patterns. We focus on the setting in which the required linear transformation is associated with a maximum distance separable (MDS) matrix. In particular, we require that the matrix of coefficients pertaining to the required linear combinations is the generator matrix of an MDS code. We establish lower and upper bounds on the capacity of PLT with individual privacy, where the capacity is defined as the supremum of all achievable download rates. We show that our bounds are tight under certain conditions.

Single-Server Private Linear Transformation: The Joint Privacy Case

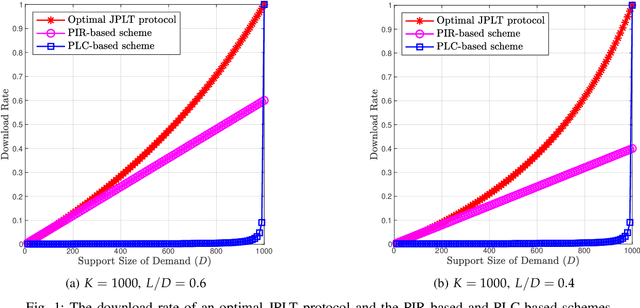
This paper introduces the problem of Private Linear Transformation (PLT) which generalizes the problems of private information retrieval and private linear computation. The PLT problem includes one or more remote server(s) storing (identical copies of) $K$ messages and a user who wants to compute $L$ independent linear combinations of a $D$-subset of messages. The objective of the user is to perform the computation by downloading minimum possible amount of information from the server(s), while protecting the identities of the $D$ messages required for the computation. In this work, we focus on the single-server setting of the PLT problem when the identities of the $D$ messages required for the computation must be protected jointly. We consider two different models, depending on whether the coefficient matrix of the required $L$ linear combinations generates a Maximum Distance Separable (MDS) code. We prove that the capacity for both models is given by $L/(K-D+L)$, where the capacity is defined as the supremum of all achievable download rates. Our converse proofs are based on linear-algebraic and information-theoretic arguments that establish connections between PLT schemes and linear codes. We also present an achievability scheme for each of the models being considered.

Private Linear Transformation: The Individual Privacy Case

This paper considers the single-server Private Linear Transformation (PLT) problem when individual privacy is required. In this problem, there is a user that wishes to obtain $L$ linear combinations of a $D$-subset of messages belonging to a dataset of $K$ messages stored on a single server. The goal is to minimize the download cost while keeping the identity of every message required for the computation individually private. The individual privacy requirement implies that, from the perspective of the server, every message is equally likely to belong to the $D$-subset of messages that constitute the support set of the required linear combinations. We focus on the setting in which the matrix of coefficients pertaining to the required linear combinations is the generator matrix of a Maximum Distance Separable code. We establish lower and upper bounds on the capacity of PLT with individual privacy, where the capacity is defined as the supremum of all achievable download rates. We show that our bounds are tight under certain divisibility conditions. In addition, we present lower bounds on the capacity of the settings in which the user has a prior side information about a subset of messages.

Private Linear Transformation: The Joint Privacy Case

We introduce the problem of Private Linear Transformation (PLT). This problem includes a single (or multiple) remote server(s) storing (identical copies of) $K$ messages and a user who wants to compute $L$ linear combinations of a $D$-subset of these messages by downloading the minimum amount of information from the server(s) while protecting the privacy of the entire set of $D$ messages. This problem generalizes the Private Information Retrieval and Private Linear Computation problems. In this work, we focus on the single-server case. For the setting in which the coefficient matrix of the required $L$ linear combinations generates a Maximum Distance Separable (MDS) code, we characterize the capacity -- defined as the supremum of all achievable download rates, for all parameters $K, D, L$. In addition, we present lower and/or upper bounds on the capacity for the settings with non-MDS coefficient matrices and the settings with a prior side information.