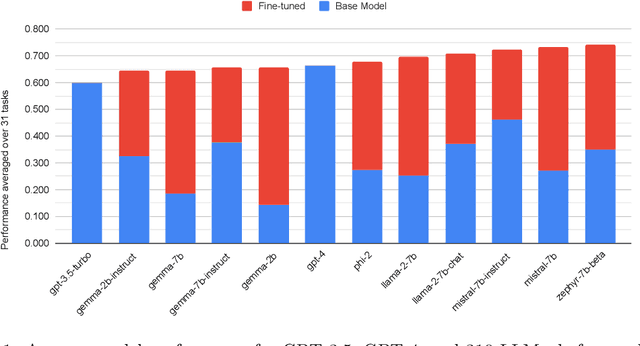
LoRA Land: 310 Fine-tuned LLMs that Rival GPT-4, A Technical Report

Low Rank Adaptation (LoRA) has emerged as one of the most widely adopted methods for Parameter Efficient Fine-Tuning (PEFT) of Large Language Models (LLMs). LoRA reduces the number of trainable parameters and memory usage while achieving comparable performance to full fine-tuning. We aim to assess the viability of training and serving LLMs fine-tuned with LoRA in real-world applications. First, we measure the quality of LLMs fine-tuned with quantized low rank adapters across 10 base models and 31 tasks for a total of 310 models. We find that 4-bit LoRA fine-tuned models outperform base models by 34 points and GPT-4 by 10 points on average. Second, we investigate the most effective base models for fine-tuning and assess the correlative and predictive capacities of task complexity heuristics in forecasting the outcomes of fine-tuning. Finally, we evaluate the latency and concurrency capabilities of LoRAX, an open-source Multi-LoRA inference server that facilitates the deployment of multiple LoRA fine-tuned models on a single GPU using shared base model weights and dynamic adapter loading. LoRAX powers LoRA Land, a web application that hosts 25 LoRA fine-tuned Mistral-7B LLMs on a single NVIDIA A100 GPU with 80GB memory. LoRA Land highlights the quality and cost-effectiveness of employing multiple specialized LLMs over a single, general-purpose LLM.

Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network

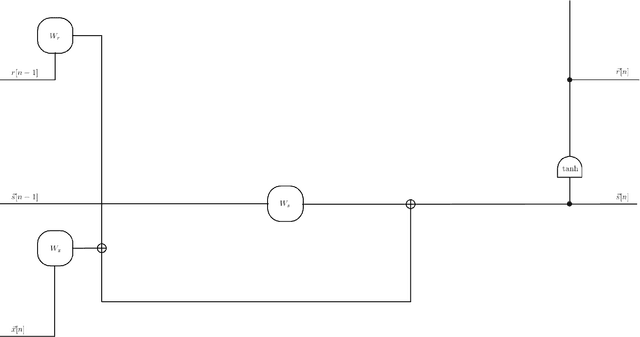
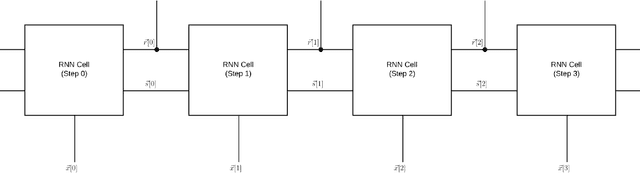
Because of their effectiveness in broad practical applications, LSTM networks have received a wealth of coverage in scientific journals, technical blogs, and implementation guides. However, in most articles, the inference formulas for the LSTM network and its parent, RNN, are stated axiomatically, while the training formulas are omitted altogether. In addition, the technique of "unrolling" an RNN is routinely presented without justification throughout the literature. The goal of this paper is to explain the essential RNN and LSTM fundamentals in a single document. Drawing from concepts in signal processing, we formally derive the canonical RNN formulation from differential equations. We then propose and prove a precise statement, which yields the RNN unrolling technique. We also review the difficulties with training the standard RNN and address them by transforming the RNN into the "Vanilla LSTM" network through a series of logical arguments. We provide all equations pertaining to the LSTM system together with detailed descriptions of its constituent entities. Albeit unconventional, our choice of notation and the method for presenting the LSTM system emphasizes ease of understanding. As part of the analysis, we identify new opportunities to enrich the LSTM system and incorporate these extensions into the Vanilla LSTM network, producing the most general LSTM variant to date. The target reader has already been exposed to RNNs and LSTM networks through numerous available resources and is open to an alternative pedagogical approach. A Machine Learning practitioner seeking guidance for implementing our new augmented LSTM model in software for experimentation and research will find the insights and derivations in this tutorial valuable as well.