Subgroup analysis methods for time-to-event outcomes in heterogeneous randomized controlled trials

Non-significant randomized control trials can hide subgroups of good responders to experimental drugs, thus hindering subsequent development. Identifying such heterogeneous treatment effects is key for precision medicine and many post-hoc analysis methods have been developed for that purpose. While several benchmarks have been carried out to identify the strengths and weaknesses of these methods, notably for binary and continuous endpoints, similar systematic empirical evaluation of subgroup analysis for time-to-event endpoints are lacking. This work aims to fill this gap by evaluating several subgroup analysis algorithms in the context of time-to-event outcomes, by means of three different research questions: Is there heterogeneity? What are the biomarkers responsible for such heterogeneity? Who are the good responders to treatment? In this context, we propose a new synthetic and semi-synthetic data generation process that allows one to explore a wide range of heterogeneity scenarios with precise control on the level of heterogeneity. We provide an open source Python package, available on Github, containing our generation process and our comprehensive benchmark framework. We hope this package will be useful to the research community for future investigations of heterogeneity of treatment effects and subgroup analysis methods benchmarking.

Revised Note on Learning Algorithms for Quadratic Assignment with Graph Neural Networks

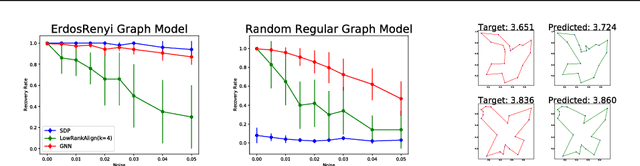
Inverse problems correspond to a certain type of optimization problems formulated over appropriate input distributions. Recently, there has been a growing interest in understanding the computational hardness of these optimization problems, not only in the worst case, but in an average-complexity sense under this same input distribution. In this revised note, we are interested in studying another aspect of hardness, related to the ability to learn how to solve a problem by simply observing a collection of previously solved instances. These 'planted solutions' are used to supervise the training of an appropriate predictive model that parametrizes a broad class of algorithms, with the hope that the resulting model will provide good accuracy-complexity tradeoffs in the average sense. We illustrate this setup on the Quadratic Assignment Problem, a fundamental problem in Network Science. We observe that data-driven models based on Graph Neural Networks offer intriguingly good performance, even in regimes where standard relaxation based techniques appear to suffer.