A practical local tomography reconstruction algorithm based on known subregion

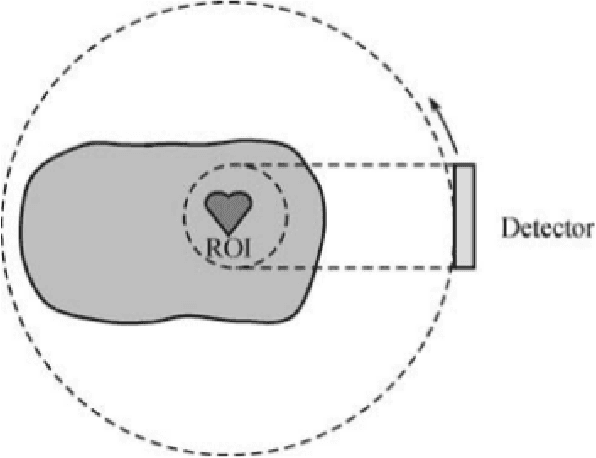
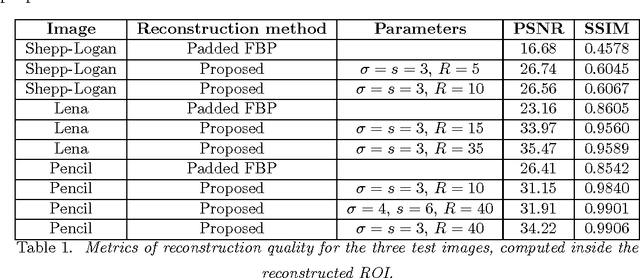
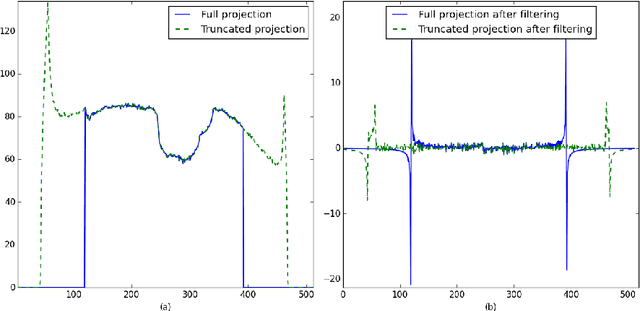
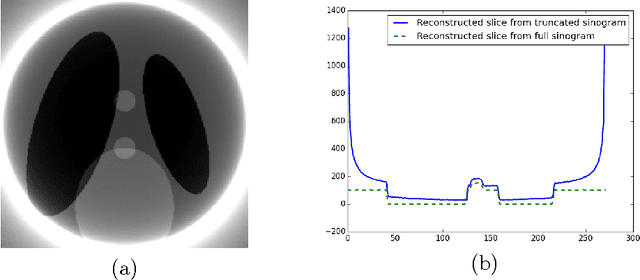
We propose a new method to reconstruct data acquired in a local tomography setup. This method uses an initial reconstruction and refines it by correcting the low frequency artifacts known as the cupping effect. A basis of Gaussian functions is used to correct the initial reconstruction. The coefficients of this basis are iteratively optimized under the constraint of a known subregion. Using a coarse basis reduces the degrees of freedom of the problem while actually correcting the cupping effect. Simulations show that the known region constraint yields an unbiased reconstruction, in accordance to uniqueness theorems stated in local tomography.

Ring artifacts correction in compressed sensing tomographic reconstruction

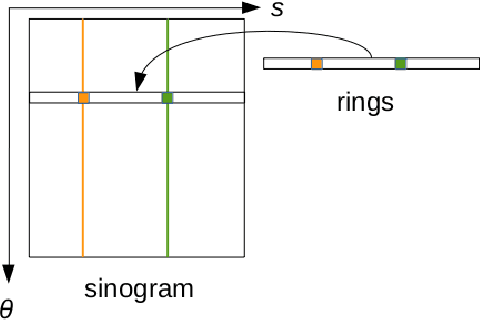
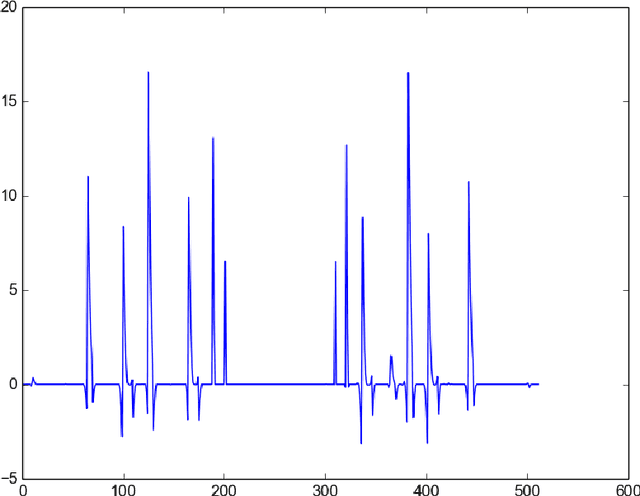
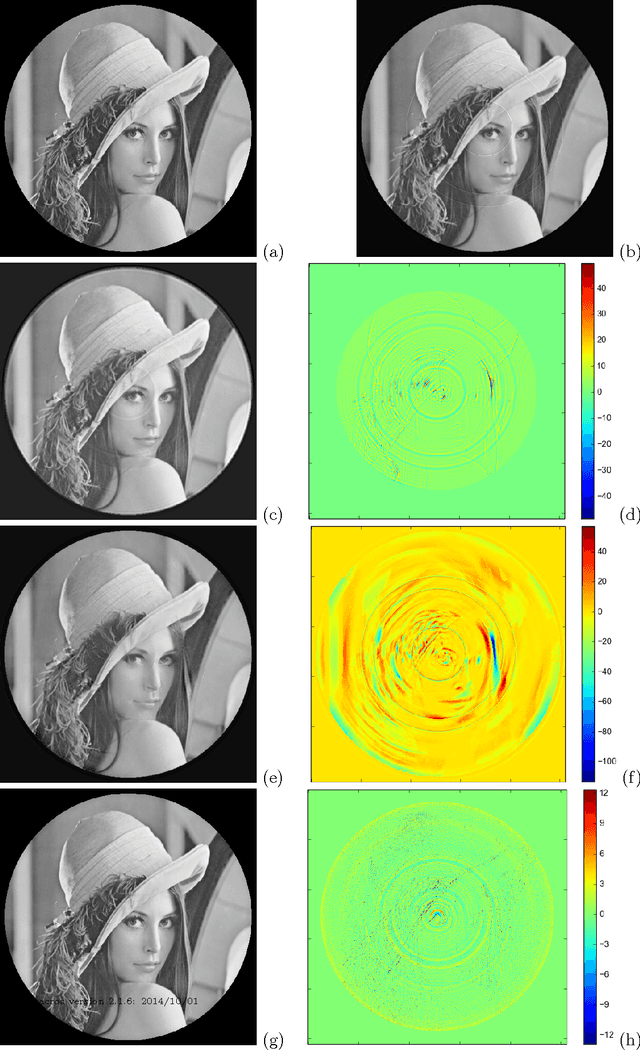
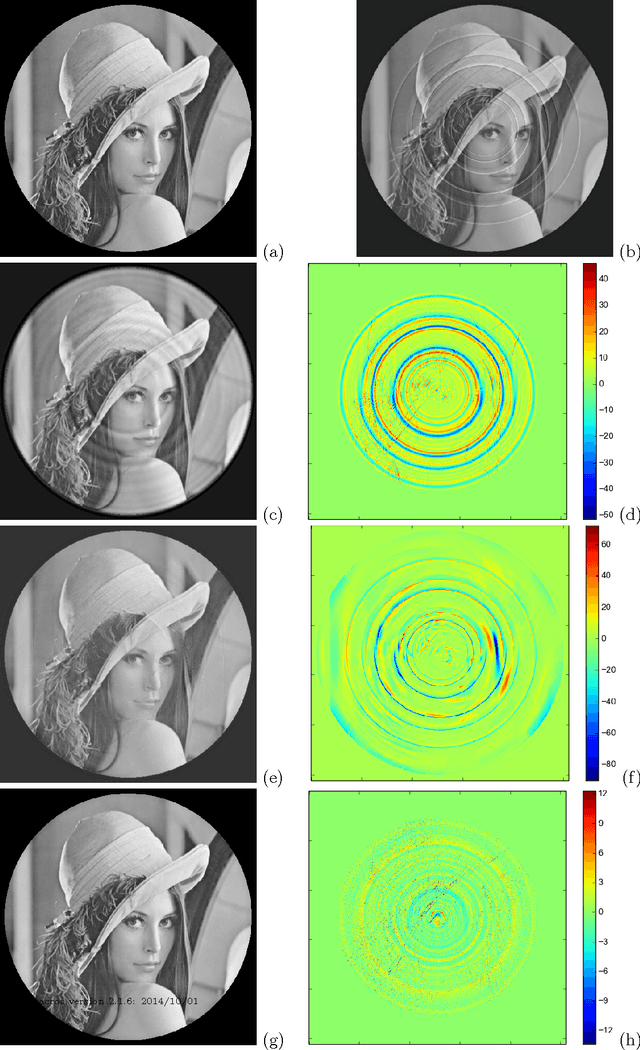
We present a novel approach to handle ring artifacts correction in compressed sensing tomographic reconstruction. The correction is part of the reconstruction process, which differs from classical sinogram pre-processing and image post-processing techniques. The principle of compressed sensing tomographic reconstruction is presented. Then, we show that the ring artifacts correction can be integrated in the reconstruction problem formalism. We provide numerical results for both simulated and real data. This technique is included in the PyHST2 code which is used at the European Synchrotron Radiation Facility for tomographic reconstruction.

PyHST2: an hybrid distributed code for high speed tomographic reconstruction with iterative reconstruction and a priori knowledge capabilities

We present the PyHST2 code which is in service at ESRF for phase-contrast and absorption tomography. This code has been engineered to sustain the high data flow typical of the third generation synchrotron facilities (10 terabytes per experiment) by adopting a distributed and pipelined architecture. The code implements, beside a default filtered backprojection reconstruction, iterative reconstruction techniques with a-priori knowledge. These latter are used to improve the reconstruction quality or in order to reduce the required data volume and reach a given quality goal. The implemented a-priori knowledge techniques are based on the total variation penalisation and a new recently found convex functional which is based on overlapping patches. We give details of the different methods and their implementations while the code is distributed under free license. We provide methods for estimating, in the absence of ground-truth data, the optimal parameters values for a-priori techniques.

A Convex Functional for Image Denoising based on Patches with Constrained Overlaps and its vectorial application to Low Dose Differential Phase Tomography

We solve the image denoising problem with a dictionary learning technique by writing a convex functional of a new form. This functional contains beside the usual sparsity inducing term and fidelity term, a new term which induces similarity between overlapping patches in the overlap regions. The functional depends on two free regularization parameters: a coefficient multiplying the sparsity-inducing $L_{1}$ norm of the patch basis functions coefficients, and a coefficient multiplying the $L_{2}$ norm of the differences between patches in the overlapping regions. The solution is found by applying the iterative proximal gradient descent method with FISTA acceleration. In the case of tomography reconstruction we calculate the gradient by applying projection of the solution and its error backprojection at each iterative step. We study the quality of the solution, as a function of the regularization parameters and noise, on synthetic datas for which the solution is a-priori known. We apply the method on experimental data in the case of Differential Phase Tomography. For this case we use an original approach which consists in using vectorial patches, each patch having two components: one per each gradient component. The resulting algorithm, implemented in the ESRF tomography reconstruction code PyHST, results to be robust, efficient, and well adapted to strongly reduce the required dose and the number of projections in medical tomography.