A practical local tomography reconstruction algorithm based on known subregion
Paper and Code
Jun 15, 2016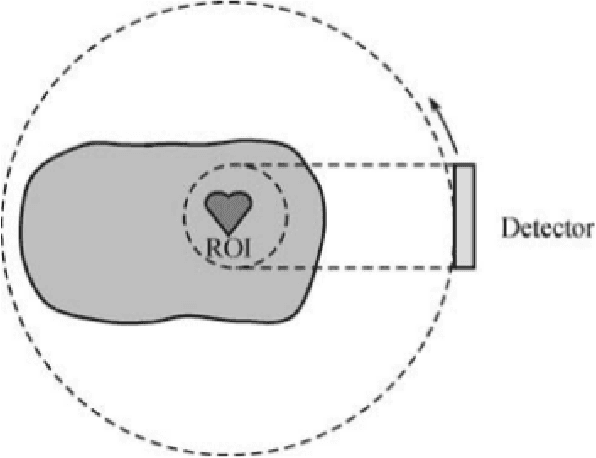
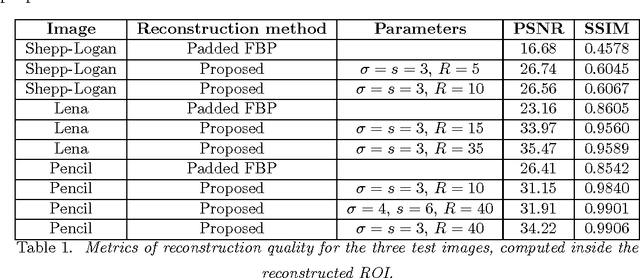
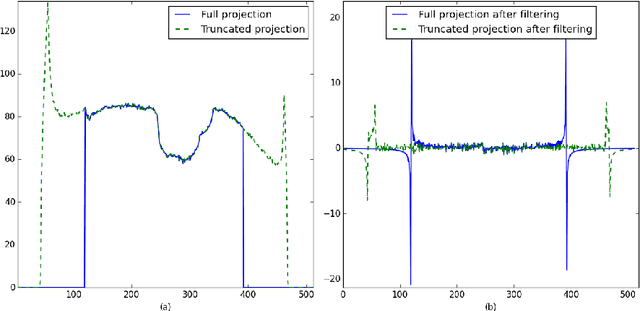
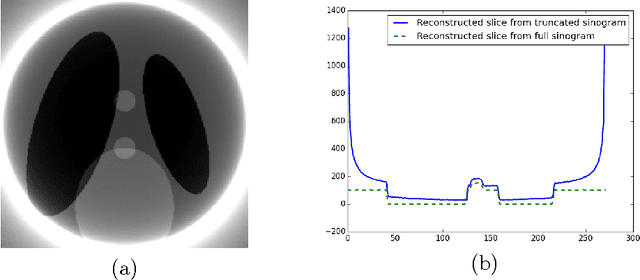
We propose a new method to reconstruct data acquired in a local tomography setup. This method uses an initial reconstruction and refines it by correcting the low frequency artifacts known as the cupping effect. A basis of Gaussian functions is used to correct the initial reconstruction. The coefficients of this basis are iteratively optimized under the constraint of a known subregion. Using a coarse basis reduces the degrees of freedom of the problem while actually correcting the cupping effect. Simulations show that the known region constraint yields an unbiased reconstruction, in accordance to uniqueness theorems stated in local tomography.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge