Aleksei Kalinov
Error Feedback Can Accurately Compress Preconditioners
Jun 16, 2023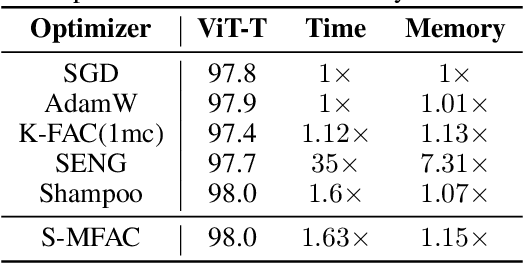
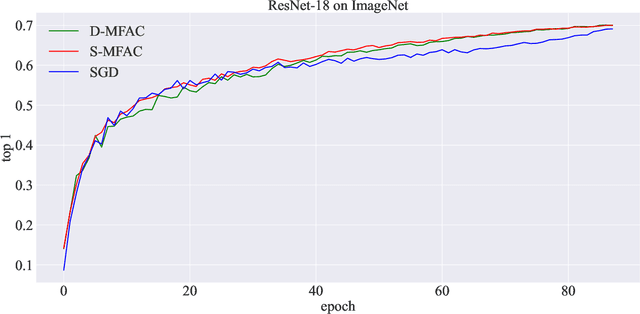
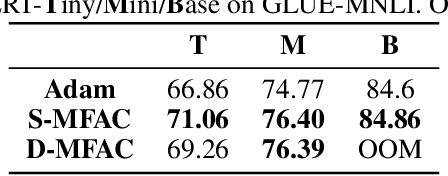
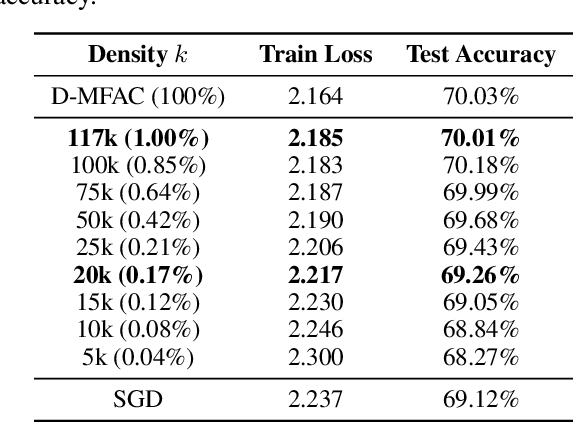
Abstract:Leveraging second-order information at the scale of deep networks is one of the main lines of approach for improving the performance of current optimizers for deep learning. Yet, existing approaches for accurate full-matrix preconditioning, such as Full-Matrix Adagrad (GGT) or Matrix-Free Approximate Curvature (M-FAC) suffer from massive storage costs when applied even to medium-scale models, as they must store a sliding window of gradients, whose memory requirements are multiplicative in the model dimension. In this paper, we address this issue via an efficient and simple-to-implement error-feedback technique that can be applied to compress preconditioners by up to two orders of magnitude in practice, without loss of convergence. Specifically, our approach compresses the gradient information via sparsification or low-rank compression \emph{before} it is fed into the preconditioner, feeding the compression error back into future iterations. Extensive experiments on deep neural networks for vision show that this approach can compress full-matrix preconditioners by up to two orders of magnitude without impact on accuracy, effectively removing the memory overhead of full-matrix preconditioning for implementations of full-matrix Adagrad (GGT) and natural gradient (M-FAC). Our code is available at https://github.com/IST-DASLab/EFCP.
CarneliNet: Neural Mixture Model for Automatic Speech Recognition
Jul 22, 2021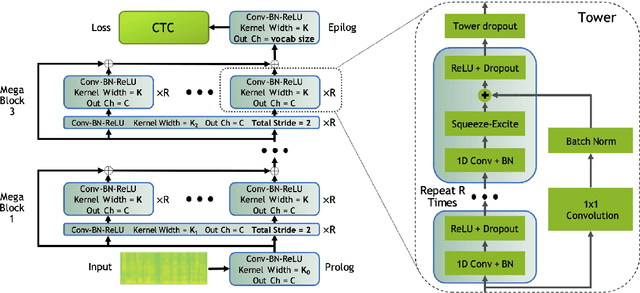
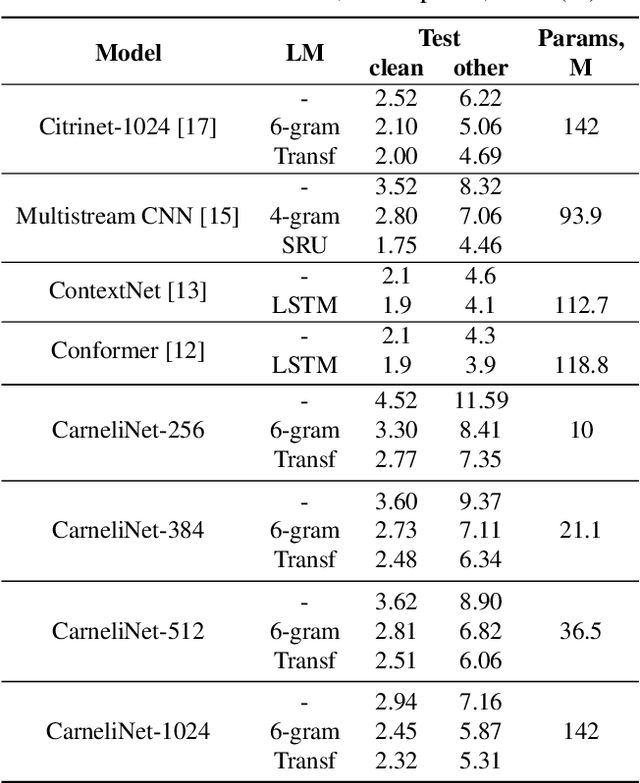
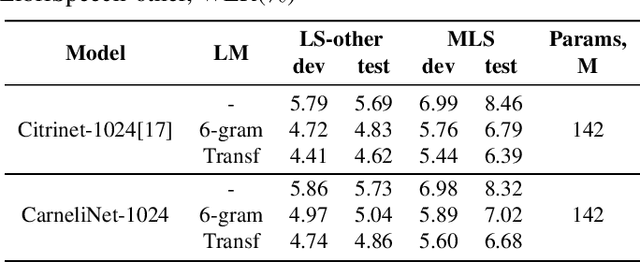
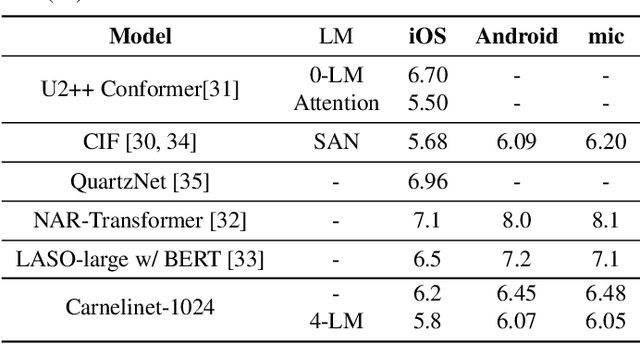
Abstract:End-to-end automatic speech recognition systems have achieved great accuracy by using deeper and deeper models. However, the increased depth comes with a larger receptive field that can negatively impact model performance in streaming scenarios. We propose an alternative approach that we call Neural Mixture Model. The basic idea is to introduce a parallel mixture of shallow networks instead of a very deep network. To validate this idea we design CarneliNet -- a CTC-based neural network composed of three mega-blocks. Each mega-block consists of multiple parallel shallow sub-networks based on 1D depthwise-separable convolutions. We evaluate the model on LibriSpeech, MLS and AISHELL-2 datasets and achieved close to state-of-the-art results for CTC-based models. Finally, we demonstrate that one can dynamically reconfigure the number of parallel sub-networks to accommodate the computational requirements without retraining.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge