Generalization error bounds for kernel matrix completion and extrapolation

Prior information can be incorporated in matrix completion to improve estimation accuracy and extrapolate the missing entries. Reproducing kernel Hilbert spaces provide tools to leverage the said prior information, and derive more reliable algorithms. This paper analyzes the generalization error of such approaches, and presents numerical tests confirming the theoretical results.

Matrix completion and extrapolation via kernel regression

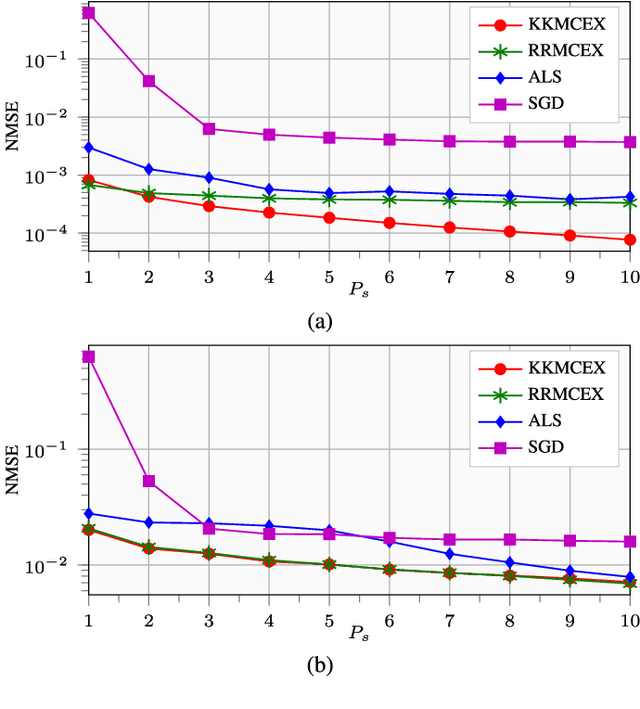
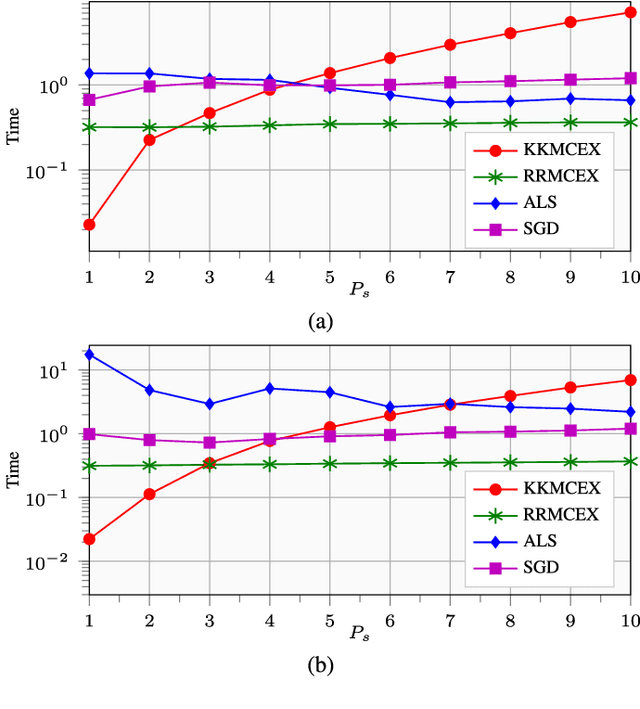
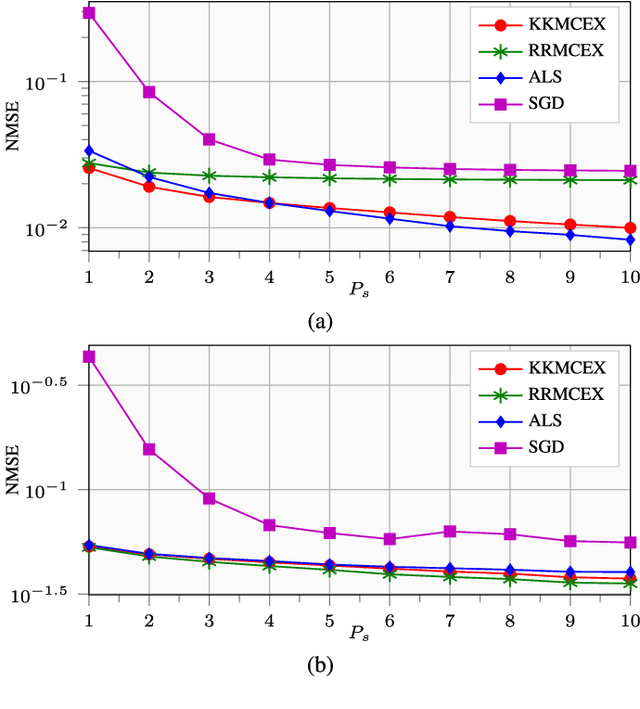
Matrix completion and extrapolation (MCEX) are dealt with here over reproducing kernel Hilbert spaces (RKHSs) in order to account for prior information present in the available data. Aiming at a faster and low-complexity solver, the task is formulated as a kernel ridge regression. The resultant MCEX algorithm can also afford online implementation, while the class of kernel functions also encompasses several existing approaches to MC with prior information. Numerical tests on synthetic and real datasets show that the novel approach performs faster than widespread methods such as alternating least squares (ALS) or stochastic gradient descent (SGD), and that the recovery error is reduced, especially when dealing with noisy data.

Blind Multiclass Ensemble Classification

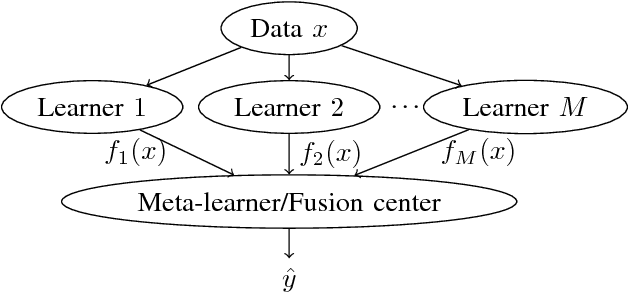
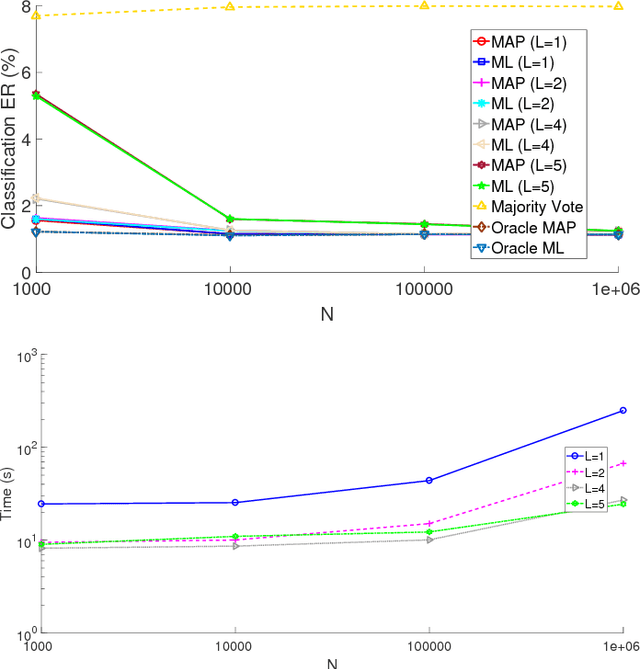
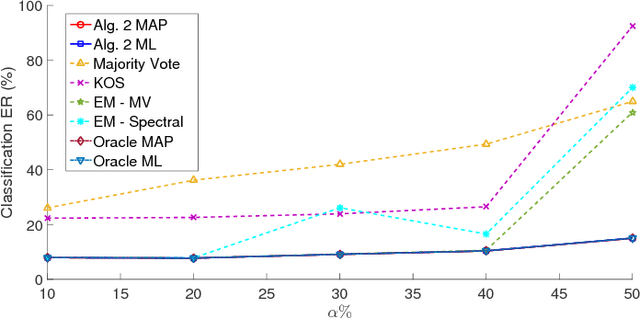
The rising interest in pattern recognition and data analytics has spurred the development of innovative machine learning algorithms and tools. However, as each algorithm has its strengths and limitations, one is motivated to judiciously fuse multiple algorithms in order to find the "best" performing one, for a given dataset. Ensemble learning aims at such high-performance meta-algorithm, by combining the outputs from multiple algorithms. The present work introduces a blind scheme for learning from ensembles of classifiers, using a moment matching method that leverages joint tensor and matrix factorization. Blind refers to the combiner who has no knowledge of the ground-truth labels that each classifier has been trained on. A rigorous performance analysis is derived and the proposed scheme is evaluated on synthetic and real datasets.