Matrix completion and extrapolation via kernel regression
Paper and Code
Aug 01, 2018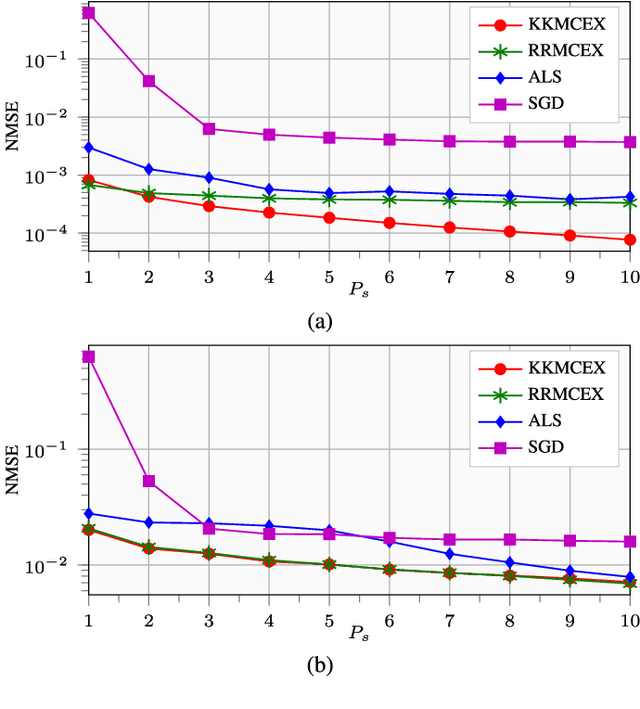
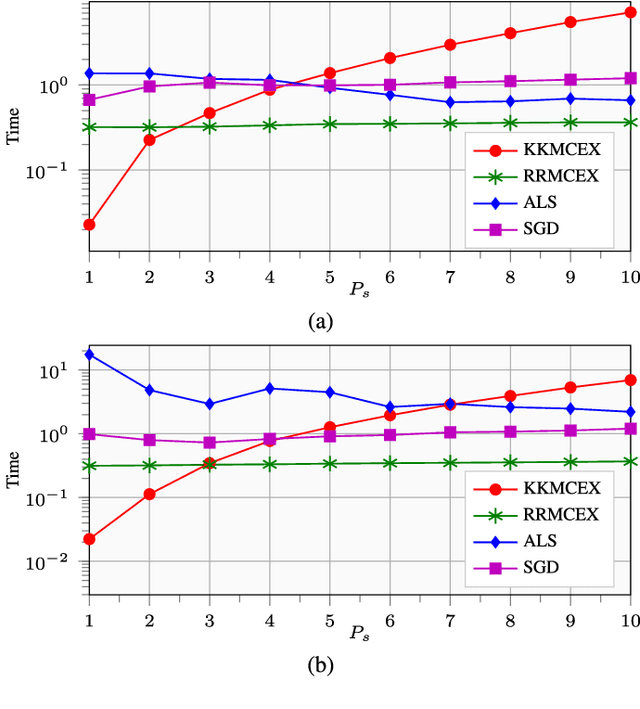
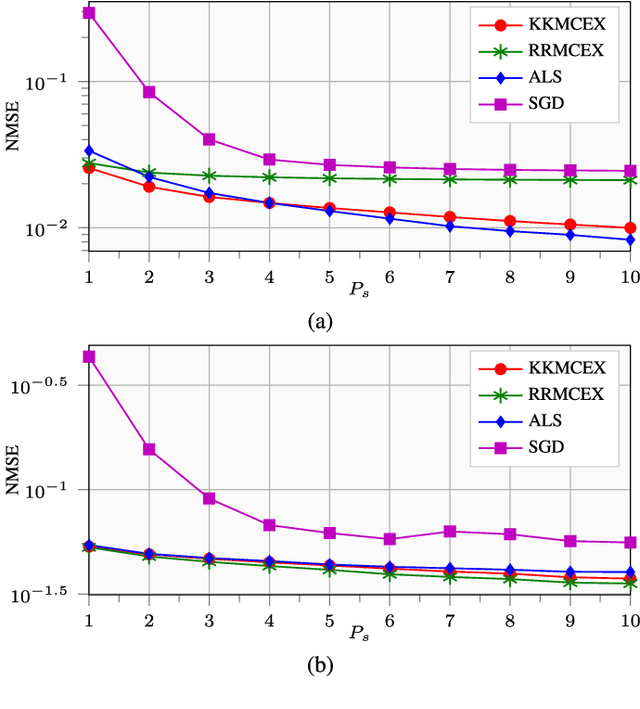

Matrix completion and extrapolation (MCEX) are dealt with here over reproducing kernel Hilbert spaces (RKHSs) in order to account for prior information present in the available data. Aiming at a faster and low-complexity solver, the task is formulated as a kernel ridge regression. The resultant MCEX algorithm can also afford online implementation, while the class of kernel functions also encompasses several existing approaches to MC with prior information. Numerical tests on synthetic and real datasets show that the novel approach performs faster than widespread methods such as alternating least squares (ALS) or stochastic gradient descent (SGD), and that the recovery error is reduced, especially when dealing with noisy data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge