Detecting Out-of-Distribution Inputs to Deep Generative Models Using a Test for Typicality

Recent work has shown that deep generative models can assign higher likelihood to out-of-distribution data sets than to their training data. We posit that this phenomenon is caused by a mismatch between the model's typical set and its areas of high probability density. In-distribution inputs should reside in the former but not necessarily in the latter, as previous work has presumed. To determine whether or not inputs reside in the typical set, we propose a statistically principled, easy-to-implement test using the empirical distribution of model likelihoods. The test is model agnostic and widely applicable, only requiring that the likelihood can be computed or closely approximated. We report experiments showing that our procedure can successfully detect the out-of-distribution sets in several of the challenging cases reported by Nalisnick et al. (2019).

Hybrid Models with Deep and Invertible Features

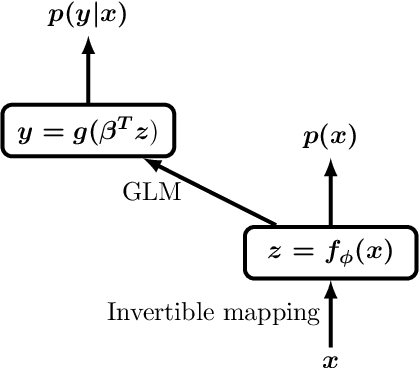
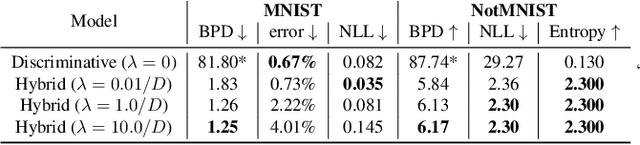
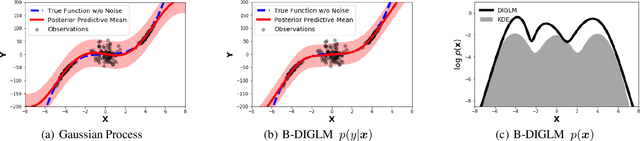
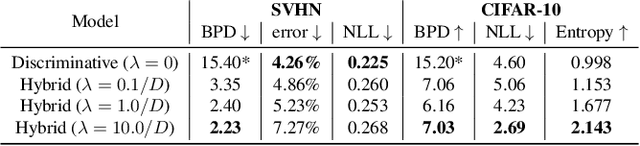
We propose a neural hybrid model consisting of a linear model defined on a set of features computed by a deep, invertible transformation (i.e. a normalizing flow). An attractive property of our model is that both p(features), the features' density, and p(targets | features), the predictive distribution, can be computed exactly in a single feed-forward pass. We show that our hybrid model, despite the invertibility constraints, achieves similar accuracy to purely predictive models. Yet the generative component remains a good model of the input features despite the hybrid optimization objective. This offers additional capabilities such as detection of out-of-distribution inputs and enabling semi-supervised learning. The availability of the exact joint density p(targets, features) also allows us to compute many quantities readily, making our hybrid model a useful building block for downstream applications of probabilistic deep learning.

Do Deep Generative Models Know What They Don't Know?

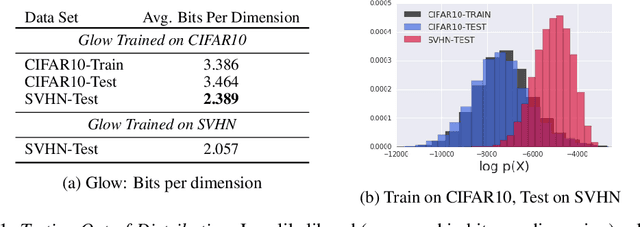
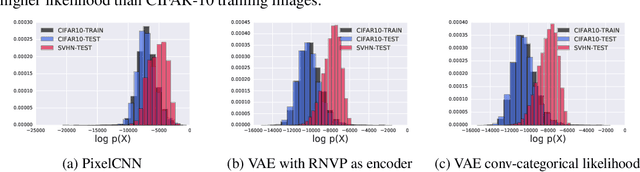
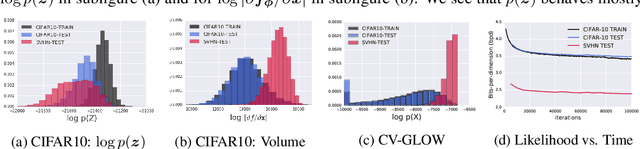
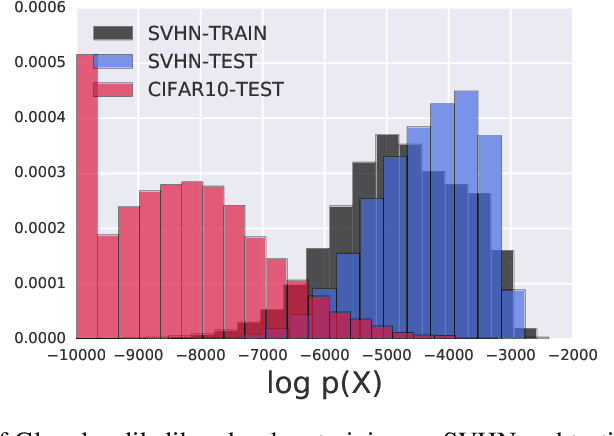
A neural network deployed in the wild may be asked to make predictions for inputs that were drawn from a different distribution than that of the training data. A plethora of work has demonstrated that it is easy to find or synthesize inputs for which a neural network is highly confident yet wrong. Generative models are widely viewed to be robust to such mistaken confidence as modeling the density of the input features can be used to detect novel, out-of-distribution inputs. In this paper we challenge this assumption. We find that the model density from flow-based models, VAEs and PixelCNN cannot distinguish images of common objects such as dogs, trucks, and horses (i.e. CIFAR-10) from those of house numbers (i.e. SVHN), assigning a higher likelihood to the latter when the model is trained on the former. We focus our analysis on flow-based generative models in particular since they are trained and evaluated via the exact marginal likelihood. We find such behavior persists even when we restrict the flow models to constant-volume transformations. These transformations admit some theoretical analysis, and we show that the difference in likelihoods can be explained by the location and variances of the data and the model curvature, which shows that such behavior is more general and not just restricted to the pairs of datasets used in our experiments. Our results caution against using the density estimates from deep generative models to identify inputs similar to the training distribution, until their behavior on out-of-distribution inputs is better understood.