Hybrid Models with Deep and Invertible Features

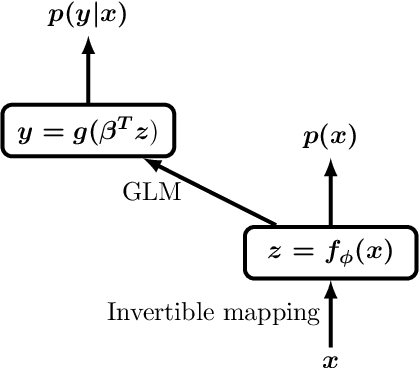
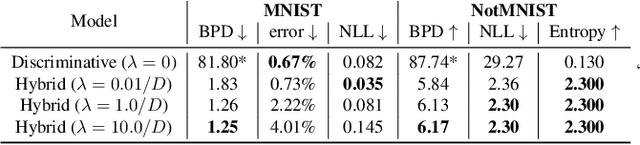
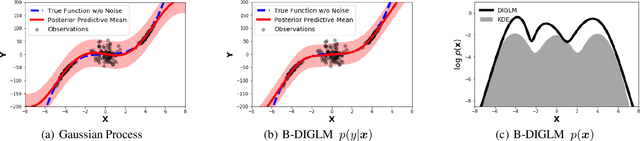
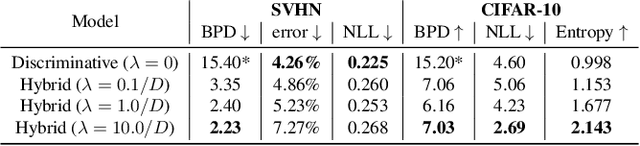
We propose a neural hybrid model consisting of a linear model defined on a set of features computed by a deep, invertible transformation (i.e. a normalizing flow). An attractive property of our model is that both p(features), the features' density, and p(targets | features), the predictive distribution, can be computed exactly in a single feed-forward pass. We show that our hybrid model, despite the invertibility constraints, achieves similar accuracy to purely predictive models. Yet the generative component remains a good model of the input features despite the hybrid optimization objective. This offers additional capabilities such as detection of out-of-distribution inputs and enabling semi-supervised learning. The availability of the exact joint density p(targets, features) also allows us to compute many quantities readily, making our hybrid model a useful building block for downstream applications of probabilistic deep learning.