Hardware-Friendly Synaptic Orders and Timescales in Liquid State Machines for Speech Classification

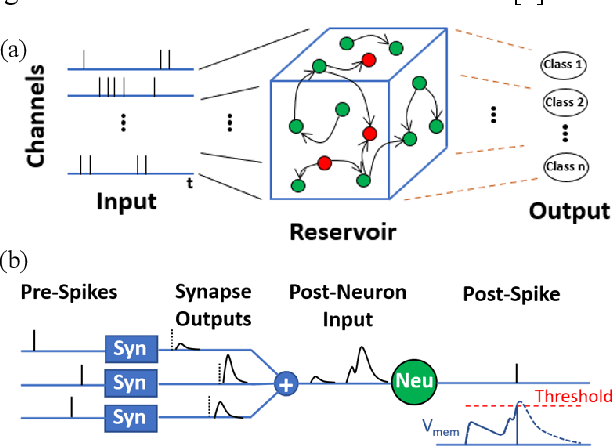
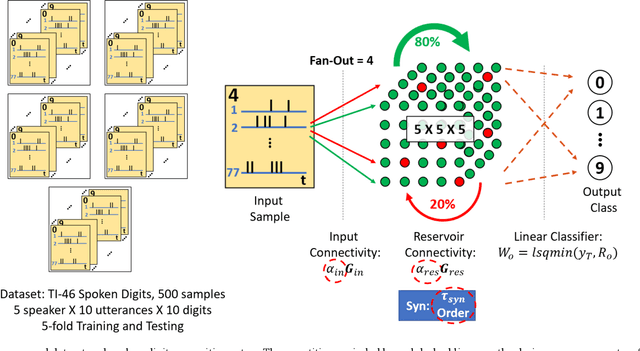
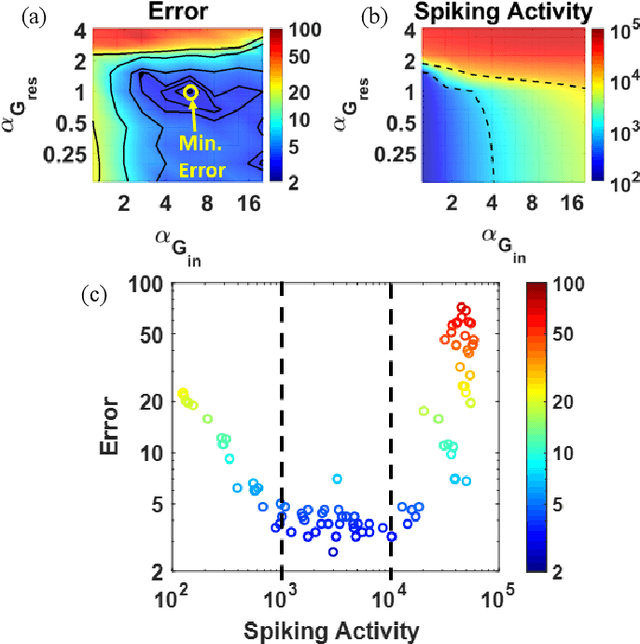
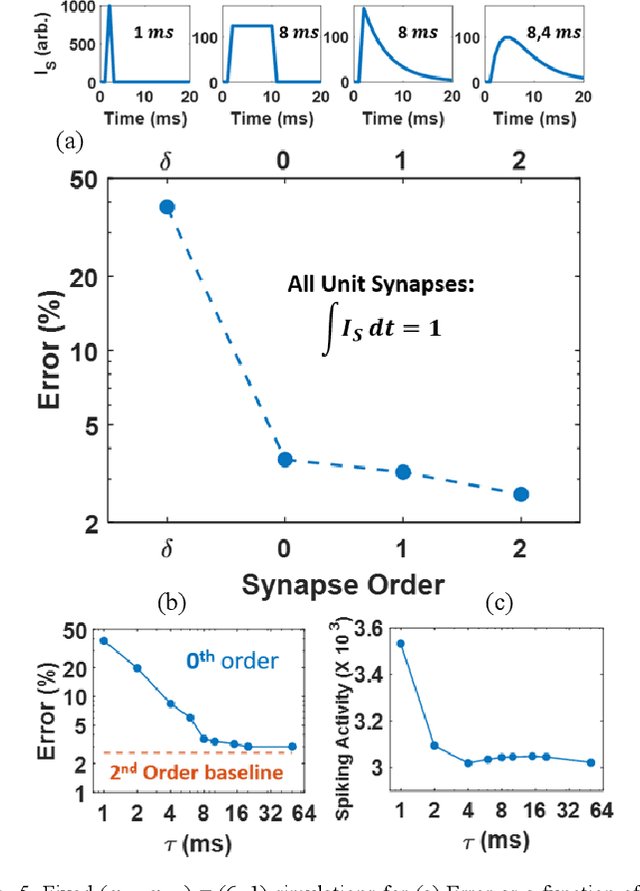
Liquid State Machines are brain inspired spiking neural networks (SNNs) with random reservoir connectivity and bio-mimetic neuronal and synaptic models. Reservoir computing networks are proposed as an alternative to deep neural networks to solve temporal classification problems. Previous studies suggest 2nd order (double exponential) synaptic waveform to be crucial for achieving high accuracy for TI-46 spoken digits recognition. The proposal of long-time range (ms) bio-mimetic synaptic waveforms is a challenge to compact and power efficient neuromorphic hardware. In this work, we analyze the role of synaptic orders namely: {\delta} (high output for single time step), 0th (rectangular with a finite pulse width), 1st (exponential fall) and 2nd order (exponential rise and fall) and synaptic timescales on the reservoir output response and on the TI-46 spoken digits classification accuracy under a more comprehensive parameter sweep. We find the optimal operating point to be correlated to an optimal range of spiking activity in the reservoir. Further, the proposed 0th order synapses perform at par with the biologically plausible 2nd order synapses. This is substantial relaxation for circuit designers as synapses are the most abundant components in an in-memory implementation for SNNs. The circuit benefits for both analog and mixed-signal realizations of 0th order synapse are highlighted demonstrating 2-3 orders of savings in area and power consumptions by eliminating Op-Amps and Digital to Analog Converter circuits. This has major implications on a complete neural network implementation with focus on peripheral limitations and algorithmic simplifications to overcome them.

Predicting Performance using Approximate State Space Model for Liquid State Machines

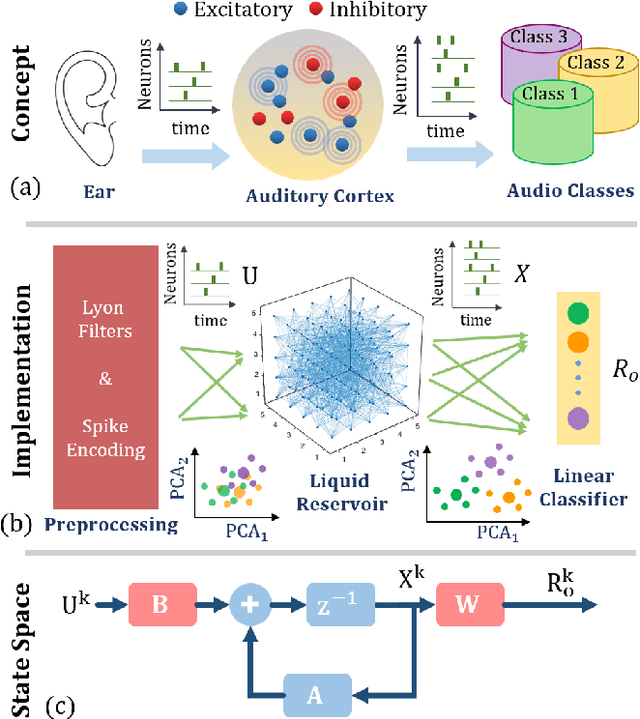
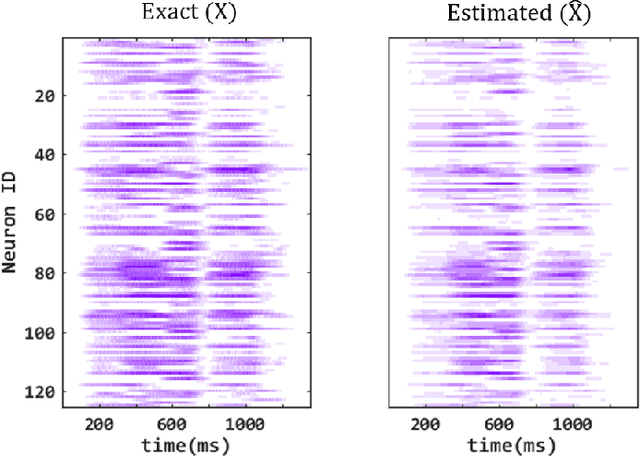
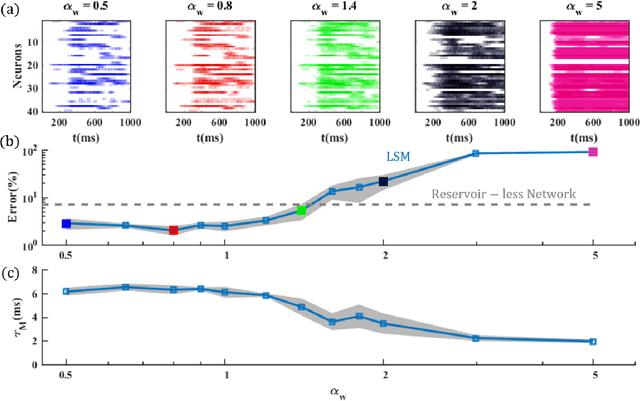
Liquid State Machine (LSM) is a brain-inspired architecture used for solving problems like speech recognition and time series prediction. LSM comprises of a randomly connected recurrent network of spiking neurons. This network propagates the non-linear neuronal and synaptic dynamics. Maass et al. have argued that the non-linear dynamics of LSMs is essential for its performance as a universal computer. Lyapunov exponent (mu), used to characterize the "non-linearity" of the network, correlates well with LSM performance. We propose a complementary approach of approximating the LSM dynamics with a linear state space representation. The spike rates from this model are well correlated to the spike rates from LSM. Such equivalence allows the extraction of a "memory" metric (tau_M) from the state transition matrix. tau_M displays high correlation with performance. Further, high tau_M system require lesser epochs to achieve a given accuracy. Being computationally cheap (1800x time efficient compared to LSM), the tau_M metric enables exploration of the vast parameter design space. We observe that the performance correlation of the tau_M surpasses the Lyapunov exponent (mu), (2-4x improvement) in the high-performance regime over multiple datasets. In fact, while mu increases monotonically with network activity, the performance reaches a maxima at a specific activity described in literature as the "edge of chaos". On the other hand, tau_M remains correlated with LSM performance even as mu increases monotonically. Hence, tau_M captures the useful memory of network activity that enables LSM performance. It also enables rapid design space exploration and fine-tuning of LSM parameters for high performance.