Probing the Robustness of Time-series Forecasting Models with CounterfacTS

A common issue for machine learning models applied to time-series forecasting is the temporal evolution of the data distributions (i.e., concept drift). Because most of the training data does not reflect such changes, the models present poor performance on the new out-of-distribution scenarios and, therefore, the impact of such events cannot be reliably anticipated ahead of time. We present and publicly release CounterfacTS, a tool to probe the robustness of deep learning models in time-series forecasting tasks via counterfactuals. CounterfacTS has a user-friendly interface that allows the user to visualize, compare and quantify time series data and their forecasts, for a number of datasets and deep learning models. Furthermore, the user can apply various transformations to the time series and explore the resulting changes in the forecasts in an interpretable manner. Through example cases, we illustrate how CounterfacTS can be used to i) identify the main features characterizing and differentiating sets of time series, ii) assess how the model performance depends on these characateristics, and iii) guide transformations of the original time series to create counterfactuals with desired properties for training and increasing the forecasting performance in new regions of the data distribution. We discuss the importance of visualizing and considering the location of the data in a projected feature space to transform time-series and create effective counterfactuals for training the models. Overall, CounterfacTS aids at creating counterfactuals to efficiently explore the impact of hypothetical scenarios not covered by the original data in time-series forecasting tasks.

Combinatorial optimization for low bit-width neural networks

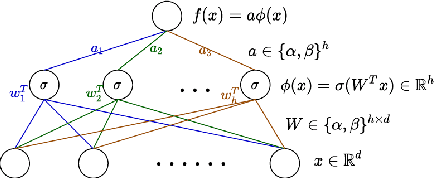
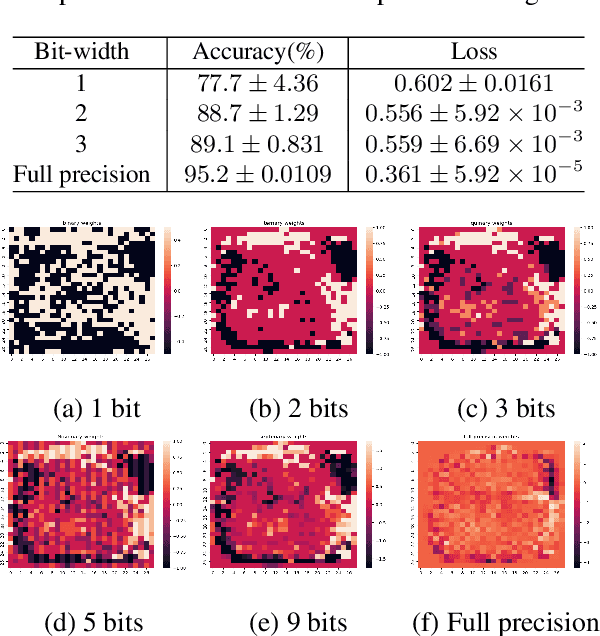
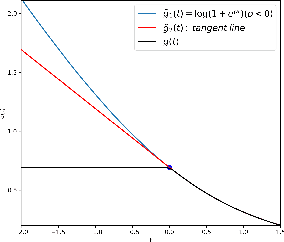
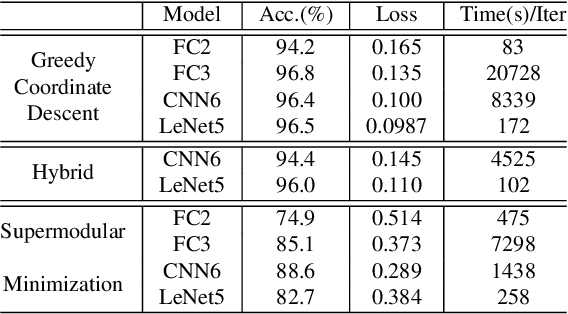
Low-bit width neural networks have been extensively explored for deployment on edge devices to reduce computational resources. Existing approaches have focused on gradient-based optimization in a two-stage train-and-compress setting or as a combined optimization where gradients are quantized during training. Such schemes require high-performance hardware during the training phase and usually store an equivalent number of full-precision weights apart from the quantized weights. In this paper, we explore methods of direct combinatorial optimization in the problem of risk minimization with binary weights, which can be made equivalent to a non-monotone submodular maximization under certain conditions. We employ an approximation algorithm for the cases with single and multilayer neural networks. For linear models, it has $\mathcal{O}(nd)$ time complexity where $n$ is the sample size and $d$ is the data dimension. We show that a combination of greedy coordinate descent and this novel approach can attain competitive accuracy on binary classification tasks.