Combinatorial optimization for low bit-width neural networks
Paper and Code
Jun 04, 2022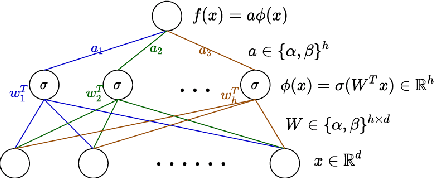
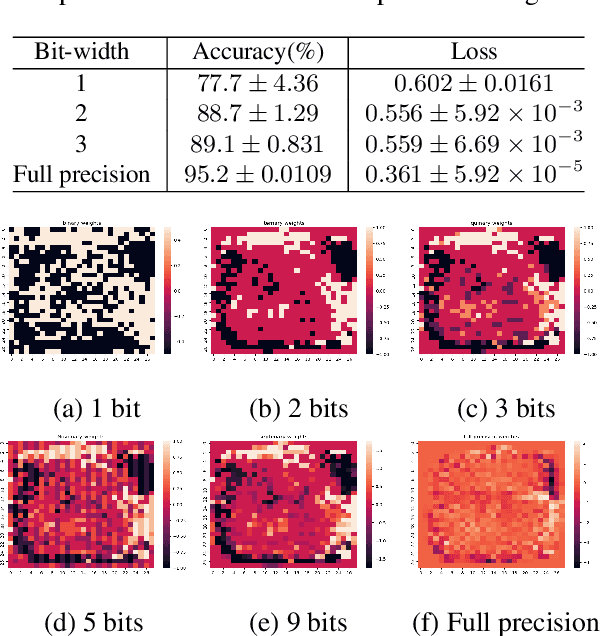
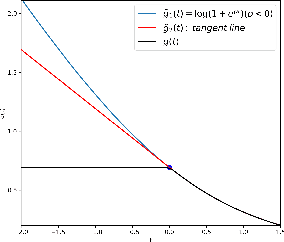
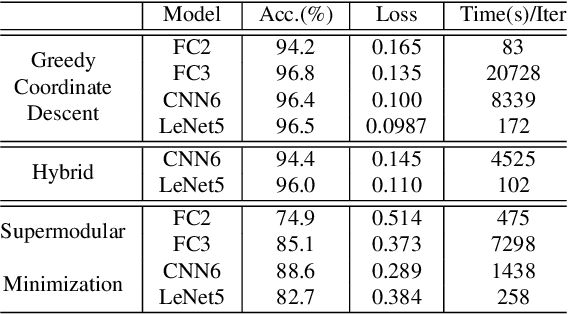
Low-bit width neural networks have been extensively explored for deployment on edge devices to reduce computational resources. Existing approaches have focused on gradient-based optimization in a two-stage train-and-compress setting or as a combined optimization where gradients are quantized during training. Such schemes require high-performance hardware during the training phase and usually store an equivalent number of full-precision weights apart from the quantized weights. In this paper, we explore methods of direct combinatorial optimization in the problem of risk minimization with binary weights, which can be made equivalent to a non-monotone submodular maximization under certain conditions. We employ an approximation algorithm for the cases with single and multilayer neural networks. For linear models, it has $\mathcal{O}(nd)$ time complexity where $n$ is the sample size and $d$ is the data dimension. We show that a combination of greedy coordinate descent and this novel approach can attain competitive accuracy on binary classification tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge