Leveraging 3D Geometric Priors in 2D Rotation Symmetry Detection

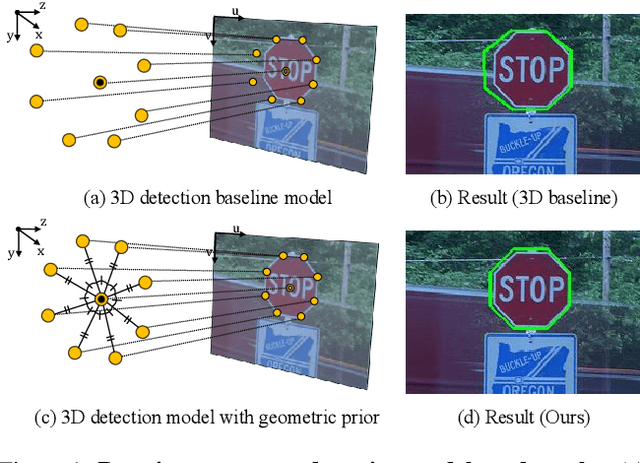
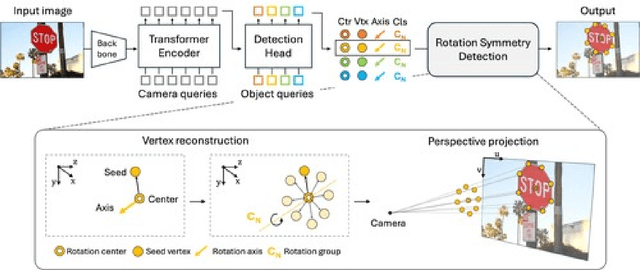
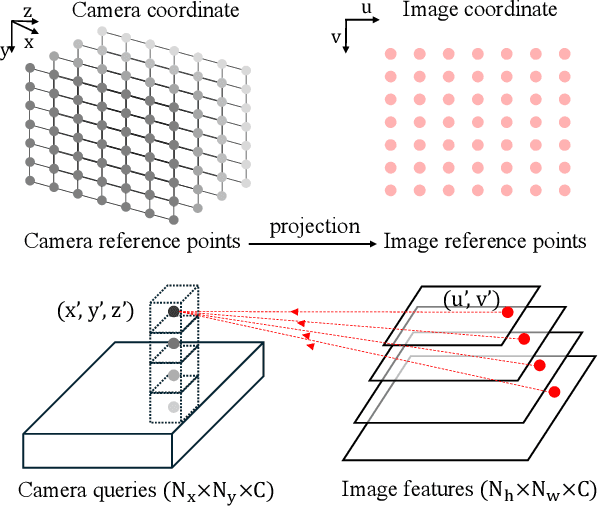
Symmetry plays a vital role in understanding structural patterns, aiding object recognition and scene interpretation. This paper focuses on rotation symmetry, where objects remain unchanged when rotated around a central axis, requiring detection of rotation centers and supporting vertices. Traditional methods relied on hand-crafted feature matching, while recent segmentation models based on convolutional neural networks detect rotation centers but struggle with 3D geometric consistency due to viewpoint distortions. To overcome this, we propose a model that directly predicts rotation centers and vertices in 3D space and projects the results back to 2D while preserving structural integrity. By incorporating a vertex reconstruction stage enforcing 3D geometric priors -- such as equal side lengths and interior angles -- our model enhances robustness and accuracy. Experiments on the DENDI dataset show superior performance in rotation axis detection and validate the impact of 3D priors through ablation studies.

Reflection and Rotation Symmetry Detection via Equivariant Learning

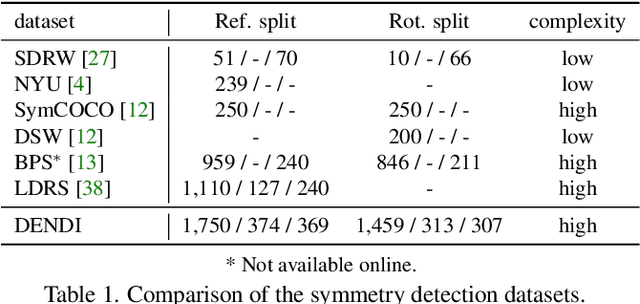
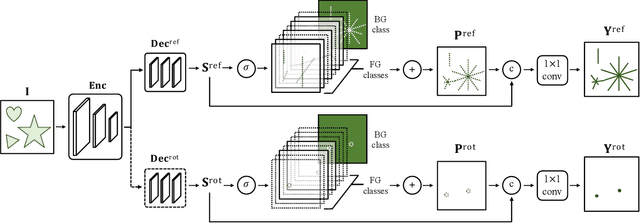
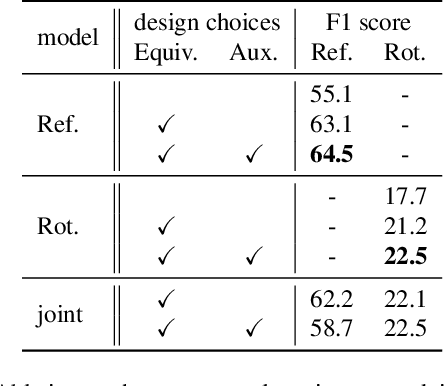
The inherent challenge of detecting symmetries stems from arbitrary orientations of symmetry patterns; a reflection symmetry mirrors itself against an axis with a specific orientation while a rotation symmetry matches its rotated copy with a specific orientation. Discovering such symmetry patterns from an image thus benefits from an equivariant feature representation, which varies consistently with reflection and rotation of the image. In this work, we introduce a group-equivariant convolutional network for symmetry detection, dubbed EquiSym, which leverages equivariant feature maps with respect to a dihedral group of reflection and rotation. The proposed network is built end-to-end with dihedrally-equivariant layers and trained to output a spatial map for reflection axes or rotation centers. We also present a new dataset, DENse and DIverse symmetry (DENDI), which mitigates limitations of existing benchmarks for reflection and rotation symmetry detection. Experiments show that our method achieves the state of the arts in symmetry detection on LDRS and DENDI datasets.

Learning to Discover Reflection Symmetry via Polar Matching Convolution

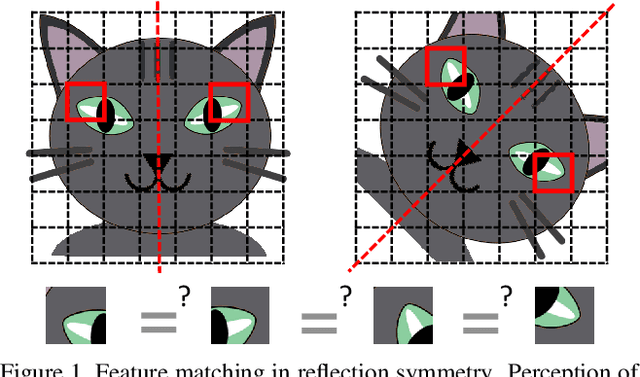
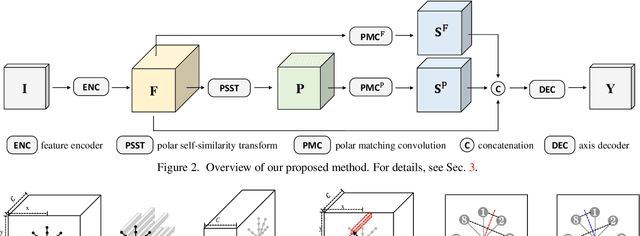
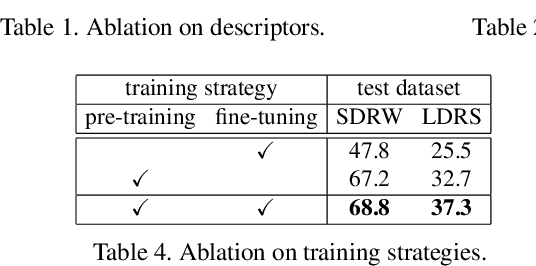
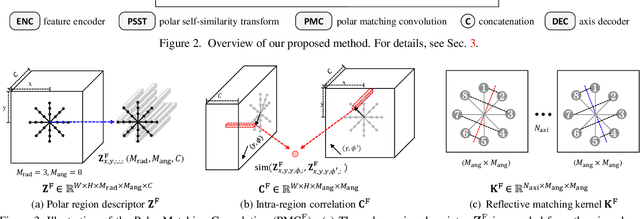
The task of reflection symmetry detection remains challenging due to significant variations and ambiguities of symmetry patterns in the wild. Furthermore, since the local regions are required to match in reflection for detecting a symmetry pattern, it is hard for standard convolutional networks, which are not equivariant to rotation and reflection, to learn the task. To address the issue, we introduce a new convolutional technique, dubbed the polar matching convolution, which leverages a polar feature pooling, a self-similarity encoding, and a systematic kernel design for axes of different angles. The proposed high-dimensional kernel convolution network effectively learns to discover symmetry patterns from real-world images, overcoming the limitations of standard convolution. In addition, we present a new dataset and introduce a self-supervised learning strategy by augmenting the dataset with synthesizing images. Experiments demonstrate that our method outperforms state-of-the-art methods in terms of accuracy and robustness.