Physics-Informed Generative Approaches for Wireless Channel Modeling

In recent years, machine learning (ML) methods have become increasingly popular in wireless communication systems for several applications. A critical bottleneck for designing ML systems for wireless communications is the availability of realistic wireless channel datasets, which are extremely resource intensive to produce. To this end, the generation of realistic wireless channels plays a key role in the subsequent design of effective ML algorithms for wireless communication systems. Generative models have been proposed to synthesize channel matrices, but outputs produced by such methods may not correspond to geometrically viable channels and do not provide any insight into the scenario of interest. In this work, we aim to address both these issues by integrating a parametric, physics-based geometric channel (PBGC) modeling framework with generative methods. To address limitations with gradient flow through the PBGC model, a linearized reformulation is presented, which ensures smooth gradient flow during generative model training, while also capturing insights about the underlying physical environment. We evaluate our model against prior baselines by comparing the generated samples in terms of the 2-Wasserstein distance and through the utility of generated data when used for downstream compression tasks.

General Total Variation Regularized Sparse Bayesian Learning for Robust Block-Sparse Signal Recovery

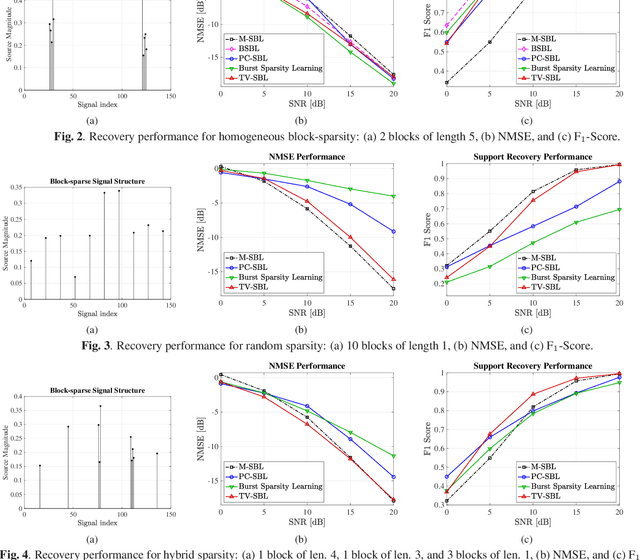
Block-sparse signal recovery without knowledge of block sizes and boundaries, such as those encountered in multi-antenna mmWave channel models, is a hard problem for compressed sensing (CS) algorithms. We propose a novel Sparse Bayesian Learning (SBL) method for block-sparse recovery based on popular CS based regularizers with the function input variable related to total variation (TV). Contrary to conventional approaches that impose the regularization on the signal components, we regularize the SBL hyperparameters. This iterative TV-regularized SBL algorithm employs a majorization-minimization approach and reduces each iteration to a convex optimization problem, enabling a flexible choice of numerical solvers. The numerical results illustrate that the TV-regularized SBL algorithm is robust to the nature of the block structure and able to recover signals with both block-patterned and isolated components, proving useful for various signal recovery systems.