How important are socioeconomic factors for hurricane performance of power systems? An analysis of disparities through machine learning

This paper investigates whether socioeconomic factors are important for the hurricane performance of the electric power system in Florida. The investigation is performed using the Random Forest classifier with Mean Decrease of Accuracy (MDA) for measuring the importance of a set of factors that include hazard intensity, time to recovery from maximum impact, and socioeconomic characteristics of the affected population. The data set (at county scale) for this study includes socioeconomic variables from the 5-year American Community Survey (ACS), as well as wind velocities, and outage data of five hurricanes including Alberto and Michael in 2018, Dorian in 2019, and Eta and Isaias in 2020. The study shows that socioeconomic variables are considerably important for the system performance model. This indicates that social disparities may exist in the occurrence of power outages, which directly impact the resilience of communities and thus require immediate attention.

Adaptive Reliability Analysis for Multi-fidelity Models using a Collective Learning Strategy

In many fields of science and engineering, models with different fidelities are available. Physical experiments or detailed simulations that accurately capture the behavior of the system are regarded as high-fidelity models with low model uncertainty, however, they are expensive to run. On the other hand, simplified physical experiments or numerical models are seen as low-fidelity models that are cheaper to evaluate. Although low-fidelity models are often not suitable for direct use in reliability analysis due to their low accuracy, they can offer information about the trend of the high-fidelity model thus providing the opportunity to explore the design space at a low cost. This study presents a new approach called adaptive multi-fidelity Gaussian process for reliability analysis (AMGPRA). Contrary to selecting training points and information sources in two separate stages as done in state-of-the-art mfEGRA method, the proposed approach finds the optimal training point and information source simultaneously using the novel collective learning function (CLF). CLF is able to assess the global impact of a candidate training point from an information source and it accommodates any learning function that satisfies a certain profile. In this context, CLF provides a new direction for quantifying the impact of new training points and can be easily extended with new learning functions to adapt to different reliability problems. The performance of the proposed method is demonstrated by three mathematical examples and one engineering problem concerning the wind reliability of transmission towers. It is shown that the proposed method achieves similar or higher accuracy with reduced computational costs compared to state-of-the-art single and multi-fidelity methods. A key application of AMGPRA is high-fidelity fragility modeling using complex and costly physics-based computational models.

Adaptive network reliability analysis: Methodology and applications to power grid

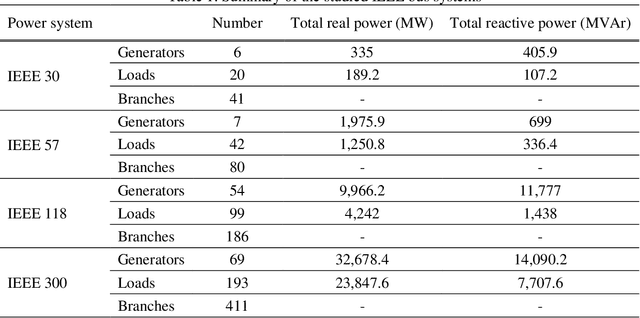
Flow network models can capture the underlying physics and operational constraints of many networked systems including the power grid and transportation and water networks. However, analyzing reliability of systems using computationally expensive flow-based models faces substantial challenges, especially for rare events. Existing actively trained meta-models, which present a new promising direction in reliability analysis, are not applicable to networks due to the inability of these methods to handle high-dimensional problems as well as discrete or mixed variable inputs. This study presents the first adaptive surrogate-based Network Reliability Analysis using Bayesian Additive Regression Trees (ANR-BART). This approach integrates BART and Monte Carlo simulation (MCS) via an active learning method that identifies the most valuable training samples based on the credible intervals derived by BART over the space of predictor variables as well as the proximity of the points to the estimated limit state. Benchmark power grids including IEEE 30, 57, 118, and 300-bus systems and their power flow models for cascading failure analysis are considered to investigate ANR-BART, MCS, subset simulation, and passively-trained optimal deep neural networks and BART. Results indicate that ANR-BART is robust and yields accurate estimates of network failure probability, while significantly reducing the computational cost of reliability analysis.

Lyapunov-based uncertainty-aware safe reinforcement learning

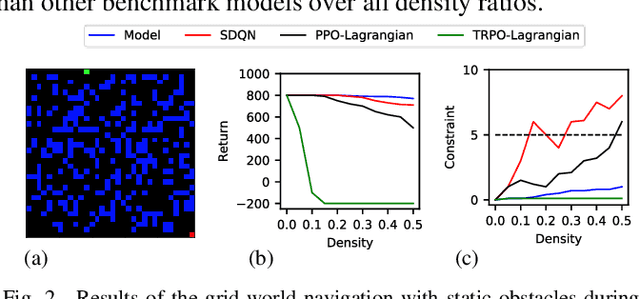
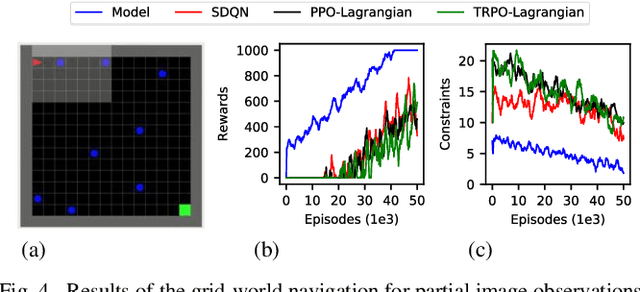
Reinforcement learning (RL) has shown a promising performance in learning optimal policies for a variety of sequential decision-making tasks. However, in many real-world RL problems, besides optimizing the main objectives, the agent is expected to satisfy a certain level of safety (e.g., avoiding collisions in autonomous driving). While RL problems are commonly formalized as Markov decision processes (MDPs), safety constraints are incorporated via constrained Markov decision processes (CMDPs). Although recent advances in safe RL have enabled learning safe policies in CMDPs, these safety requirements should be satisfied during both training and in the deployment process. Furthermore, it is shown that in memory-based and partially observable environments, these methods fail to maintain safety over unseen out-of-distribution observations. To address these limitations, we propose a Lyapunov-based uncertainty-aware safe RL model. The introduced model adopts a Lyapunov function that converts trajectory-based constraints to a set of local linear constraints. Furthermore, to ensure the safety of the agent in highly uncertain environments, an uncertainty quantification method is developed that enables identifying risk-averse actions through estimating the probability of constraint violations. Moreover, a Transformers model is integrated to provide the agent with memory to process long time horizons of information via the self-attention mechanism. The proposed model is evaluated in grid-world navigation tasks where safety is defined as avoiding static and dynamic obstacles in fully and partially observable environments. The results of these experiments show a significant improvement in the performance of the agent both in achieving optimality and satisfying safety constraints.

Value of Information Analysis via Active Learning and Knowledge Sharing in Error-Controlled Adaptive Kriging

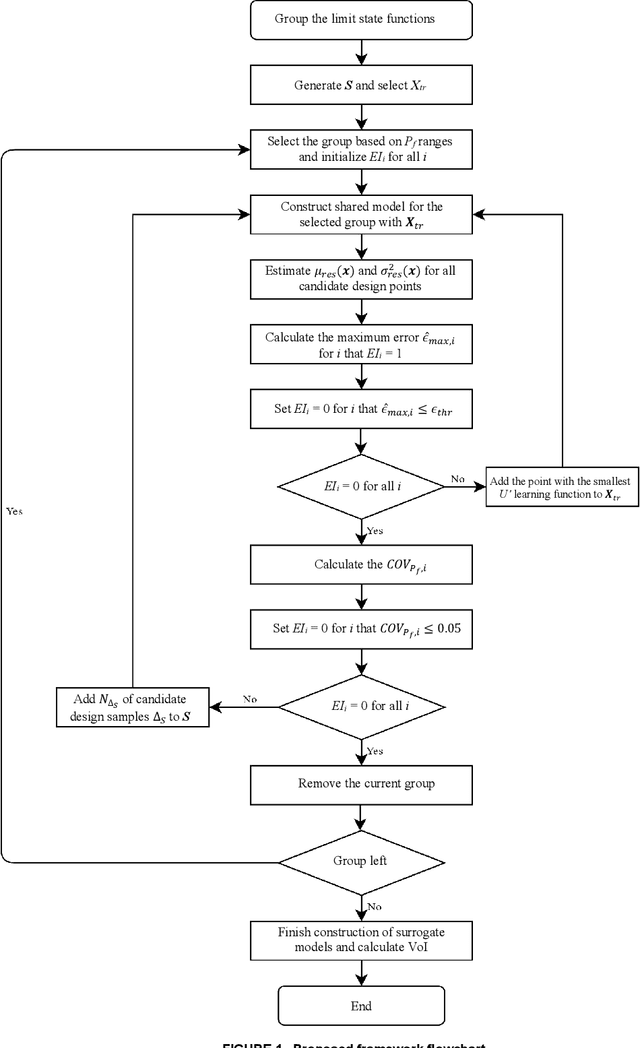
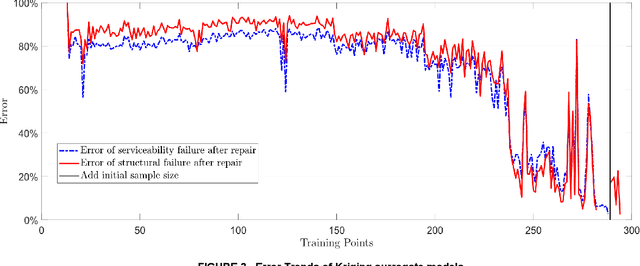
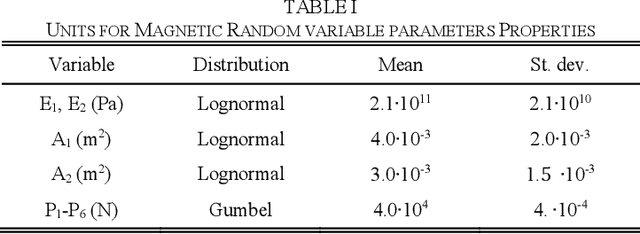
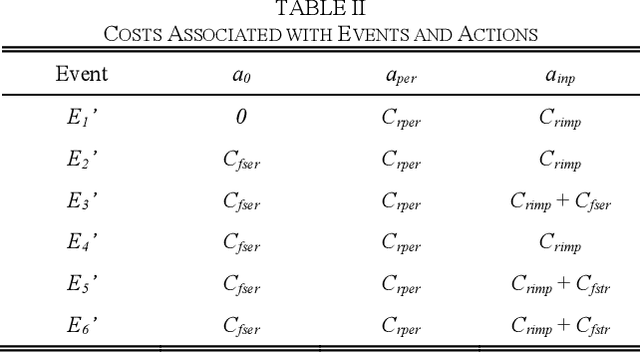
Large uncertainties in many phenomena have challenged decision making. Collecting additional information to better characterize reducible uncertainties is among decision alternatives. Value of information (VoI) analysis is a mathematical decision framework that quantifies expected potential benefits of new data and assists with optimal allocation of resources for information collection. However, analysis of VoI is computational very costly because of the underlying Bayesian inference especially for equality-type information. This paper proposes the first surrogate-based framework for VoI analysis. Instead of modeling the limit state functions describing events of interest for decision making, which is commonly pursued in surrogate model-based reliability methods, the proposed framework models system responses. This approach affords sharing equality-type information from observations among surrogate models to update likelihoods of multiple events of interest. Moreover, two knowledge sharing schemes called model and training points sharing are proposed to most effectively take advantage of the knowledge offered by costly model evaluations. Both schemes are integrated with an error rate-based adaptive training approach to efficiently generate accurate Kriging surrogate models. The proposed VoI analysis framework is applied for an optimal decision-making problem involving load testing of a truss bridge. While state-of-the-art methods based on importance sampling and adaptive Kriging Monte Carlo simulation are unable to solve this problem, the proposed method is shown to offer accurate and robust estimates of VoI with a limited number of model evaluations. Therefore, the proposed method facilitates the application of VoI for complex decision problems.

REAK: Reliability analysis through Error rate-based Adaptive Kriging

As models in various fields are becoming more complex, associated computational demands have been increasing significantly. Reliability analysis for these systems when failure probabilities are small is significantly challenging, requiring a large number of costly simulations. To address this challenge, this paper introduces Reliability analysis through Error rate-based Adaptive Kriging (REAK). An extension of the Central Limit Theorem based on Lindeberg condition is adopted here to derive the distribution of the number of design samples with wrong sign estimate and subsequently determine the maximum error rate for failure probability estimates. This error rate enables optimal establishment of effective sampling regions at each stage of an adaptive scheme for strategic generation of design samples. Moreover, it facilitates setting a target accuracy for failure probability estimation, which is used as stopping criterion for reliability analysis. These capabilities together can significantly reduce the number of calls to sophisticated, computationally demanding models. The application of REAK for four examples with varying extent of nonlinearity and dimension is presented. Results indicate that REAK is able to reduce the computational demand by as high as 50% compared to state-of-the-art methods of Adaptive Kriging with Monte Carlo Simulation (AK-MCS) and Improved Sequential Kriging Reliability Analysis (ISKRA).