Adaptive network reliability analysis: Methodology and applications to power grid

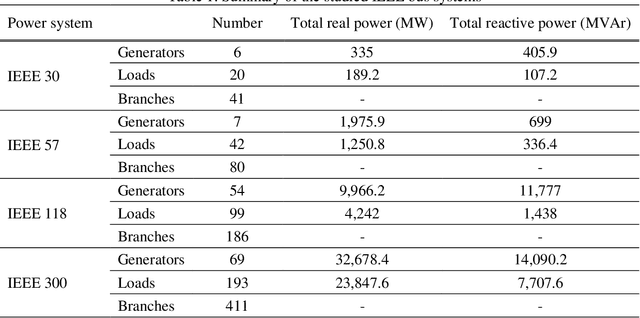
Flow network models can capture the underlying physics and operational constraints of many networked systems including the power grid and transportation and water networks. However, analyzing reliability of systems using computationally expensive flow-based models faces substantial challenges, especially for rare events. Existing actively trained meta-models, which present a new promising direction in reliability analysis, are not applicable to networks due to the inability of these methods to handle high-dimensional problems as well as discrete or mixed variable inputs. This study presents the first adaptive surrogate-based Network Reliability Analysis using Bayesian Additive Regression Trees (ANR-BART). This approach integrates BART and Monte Carlo simulation (MCS) via an active learning method that identifies the most valuable training samples based on the credible intervals derived by BART over the space of predictor variables as well as the proximity of the points to the estimated limit state. Benchmark power grids including IEEE 30, 57, 118, and 300-bus systems and their power flow models for cascading failure analysis are considered to investigate ANR-BART, MCS, subset simulation, and passively-trained optimal deep neural networks and BART. Results indicate that ANR-BART is robust and yields accurate estimates of network failure probability, while significantly reducing the computational cost of reliability analysis.

Lyapunov-based uncertainty-aware safe reinforcement learning

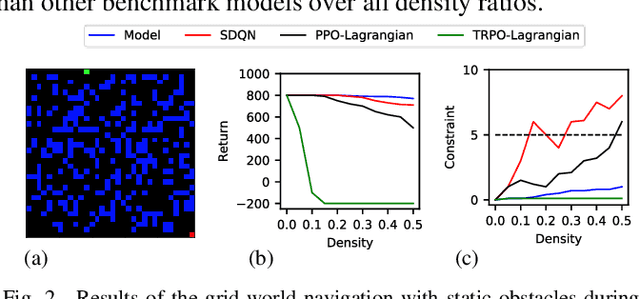
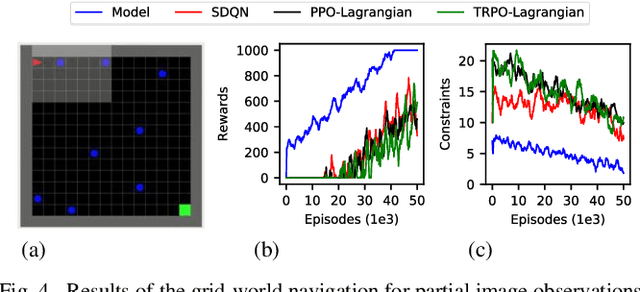
Reinforcement learning (RL) has shown a promising performance in learning optimal policies for a variety of sequential decision-making tasks. However, in many real-world RL problems, besides optimizing the main objectives, the agent is expected to satisfy a certain level of safety (e.g., avoiding collisions in autonomous driving). While RL problems are commonly formalized as Markov decision processes (MDPs), safety constraints are incorporated via constrained Markov decision processes (CMDPs). Although recent advances in safe RL have enabled learning safe policies in CMDPs, these safety requirements should be satisfied during both training and in the deployment process. Furthermore, it is shown that in memory-based and partially observable environments, these methods fail to maintain safety over unseen out-of-distribution observations. To address these limitations, we propose a Lyapunov-based uncertainty-aware safe RL model. The introduced model adopts a Lyapunov function that converts trajectory-based constraints to a set of local linear constraints. Furthermore, to ensure the safety of the agent in highly uncertain environments, an uncertainty quantification method is developed that enables identifying risk-averse actions through estimating the probability of constraint violations. Moreover, a Transformers model is integrated to provide the agent with memory to process long time horizons of information via the self-attention mechanism. The proposed model is evaluated in grid-world navigation tasks where safety is defined as avoiding static and dynamic obstacles in fully and partially observable environments. The results of these experiments show a significant improvement in the performance of the agent both in achieving optimality and satisfying safety constraints.