The Connection Between R-Learning and Inverse-Variance Weighting for Estimation of Heterogeneous Treatment Effects

Our motivation is to shed light the performance of the widely popular "R-Learner." Like many other methods for estimating conditional average treatment effects (CATEs), R-Learning can be expressed as a weighted pseudo-outcome regression (POR). Previous comparisons of POR techniques have paid careful attention to the choice of pseudo-outcome transformation. However, we argue that the dominant driver of performance is actually the choice of weights. Specifically, we argue that R-Learning implicitly performs an inverse-variance weighted form of POR. These weights stabilize the regression and allow for convenient simplifications of bias terms.

Gaussian Latent Dirichlet Allocation for Discrete Human State Discovery

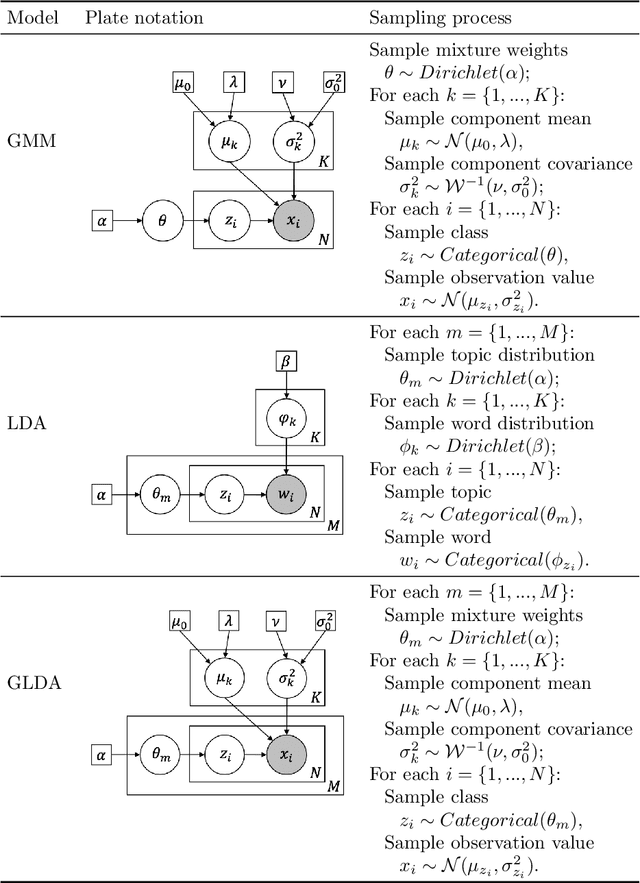
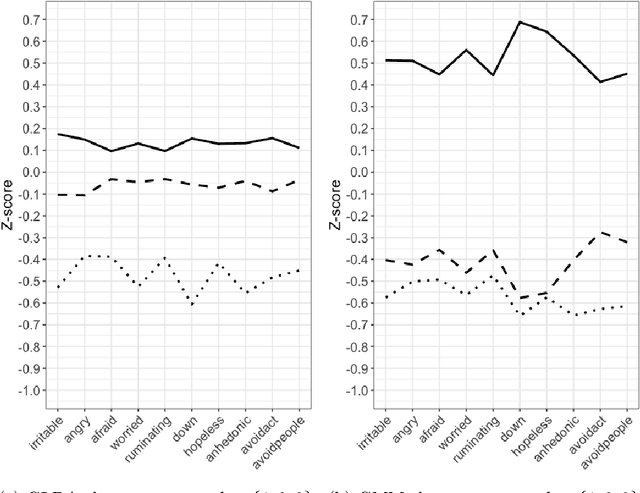
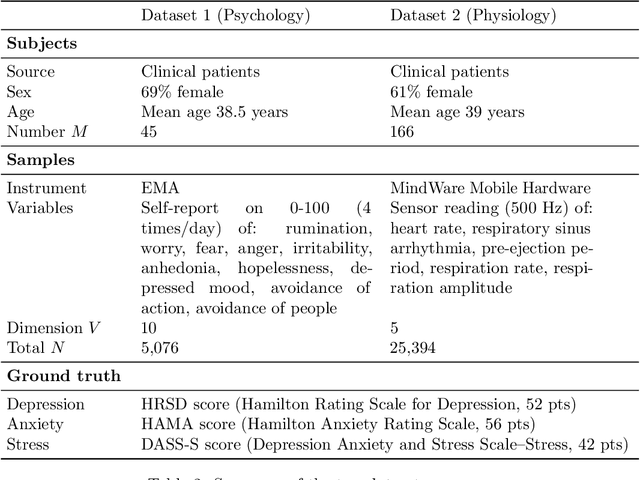
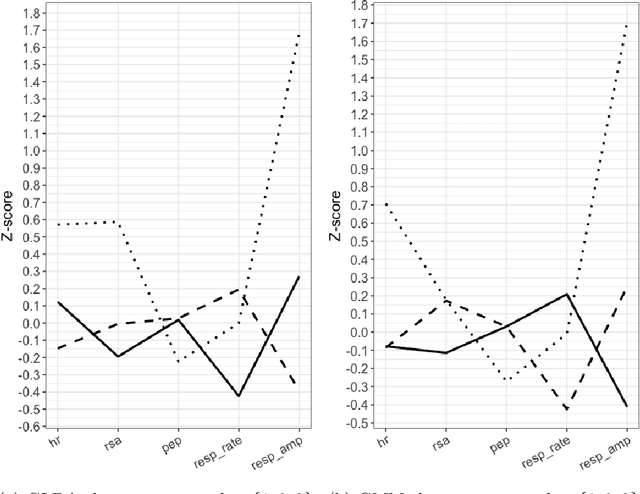
In this article we propose and validate an unsupervised probabilistic model, Gaussian Latent Dirichlet Allocation (GLDA), for the problem of discrete state discovery from repeated, multivariate psychophysiological samples collected from multiple, inherently distinct, individuals. Psychology and medical research heavily involves measuring potentially related but individually inconclusive variables from a cohort of participants to derive diagnosis, necessitating clustering analysis. Traditional probabilistic clustering models such as Gaussian Mixture Model (GMM) assume a global mixture of component distributions, which may not be realistic for observations from different patients. The GLDA model borrows the individual-specific mixture structure from a popular topic model Latent Dirichlet Allocation (LDA) in Natural Language Processing and merges it with the Gaussian component distributions of GMM to suit continuous type data. We implemented GLDA using STAN (a probabilistic modeling language) and applied it on two datasets, one containing Ecological Momentary Assessments (EMA) and the other heart measures from electrocardiogram and impedance cardiograph. We found that in both datasets the GLDA-learned class weights achieved significantly higher correlations with clinically assessed depression, anxiety, and stress scores than those produced by the baseline GMM. Our findings demonstrate the advantage of GLDA over conventional finite mixture models for human state discovery from repeated multivariate data, likely due to better characterization of potential underlying between-participant differences. Future work is required to validate the utility of this model on a broader range of applications.

SAFFRON and LORD Ensure Online Control of the False Discovery Rate Under Positive Dependence

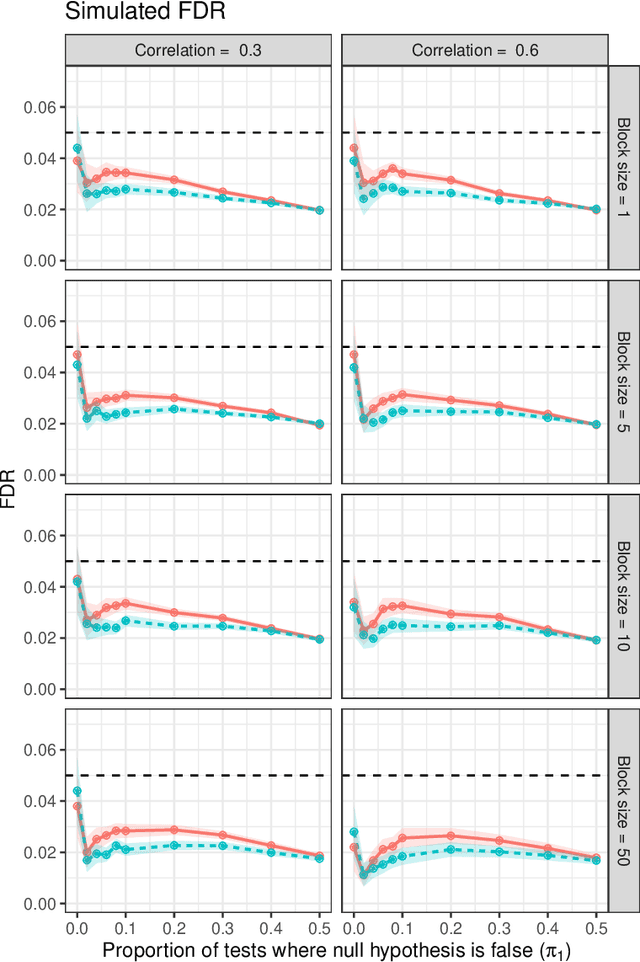
Online testing procedures assume that hypotheses are observed in sequence, and allow the significance thresholds for upcoming tests to depend on the test statistics observed so far. Some of the most popular online methods include alpha investing, LORD++ (hereafter, LORD), and SAFFRON. These three methods have been shown to provide online control of the "modified" false discovery rate (mFDR). However, to our knowledge, they have only been shown to control the traditional false discovery rate (FDR) under an independence condition on the test statistics. Our work bolsters these results by showing that SAFFRON and LORD additionally ensure online control of the FDR under nonnegative dependence. Because alpha investing can be recovered as a special case of the SAFFRON framework, the same result applies to this method as well. Our result also allows for certain forms of adaptive stopping times, for example, stopping after a certain number of rejections have been observed. For convenience, we also provide simplified versions of the LORD and SAFFRON algorithms based on geometric alpha allocations.

Online Control of the False Discovery Rate under "Decision Deadlines"

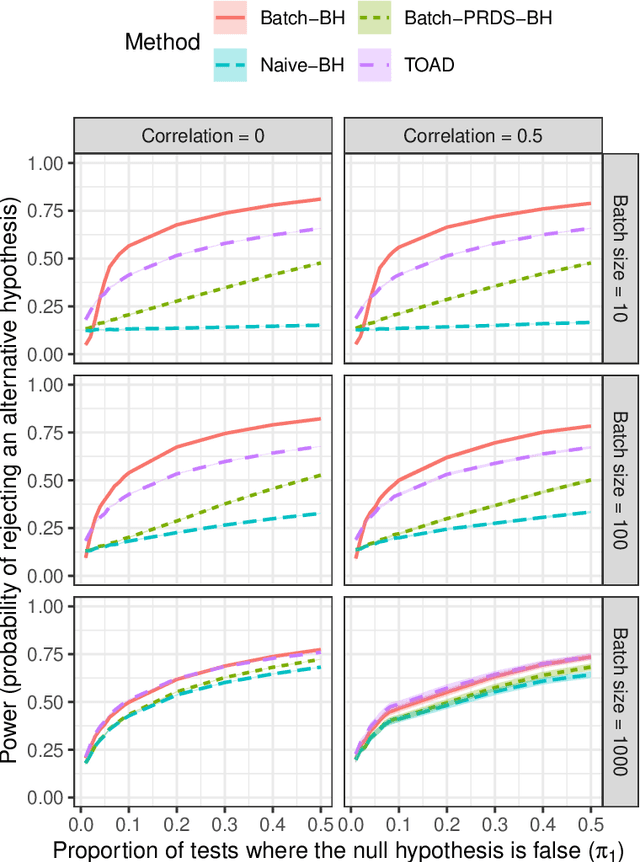
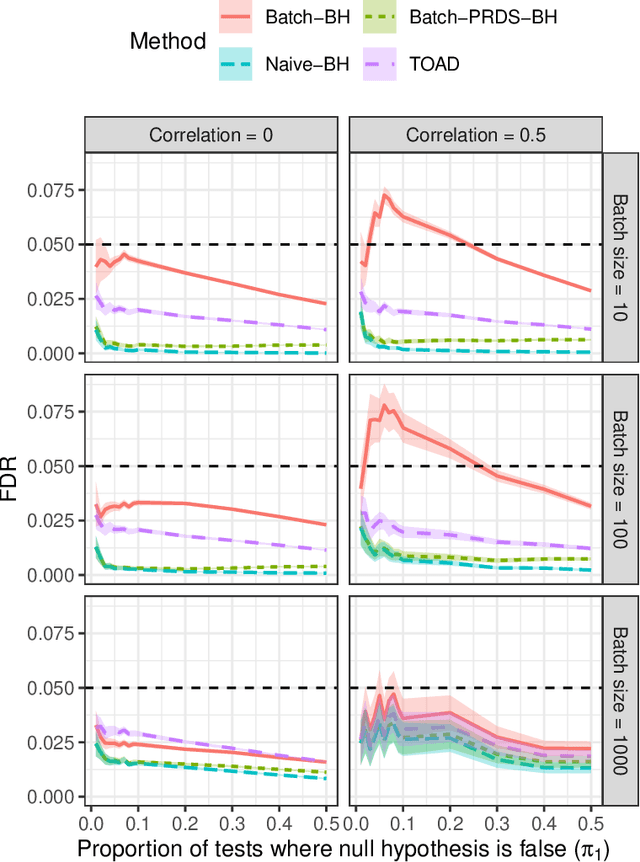
Online testing procedures aim to control the extent of false discoveries over a sequence of hypothesis tests, allowing for the possibility that early-stage test results influence the choice of hypotheses to be tested in later stages. Typically, online methods assume that a permanent decision regarding the current test (reject or not reject) must be made before advancing to the next test. We instead assume that each hypothesis requires an immediate preliminary decision, but also allows us to update that decision until a preset deadline. Roughly speaking, this lets us apply a Benjamini-Hochberg-type procedure over a moving window of hypotheses, where the threshold parameters for upcoming tests can be determined based on preliminary results. Our method controls the false discovery rate (FDR) at every stage of testing, as well as at adaptively chosen stopping times. These results apply even under arbitrary p-value dependency structures.

Optimizing Rescoring Rules with Interpretable Representations of Long-Term Information

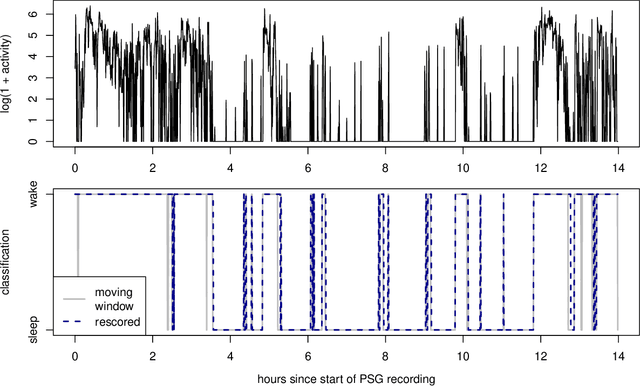
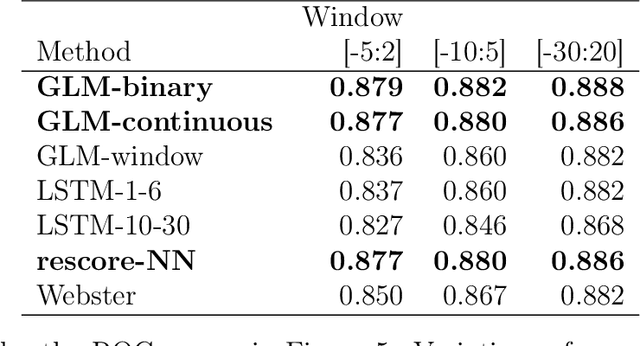
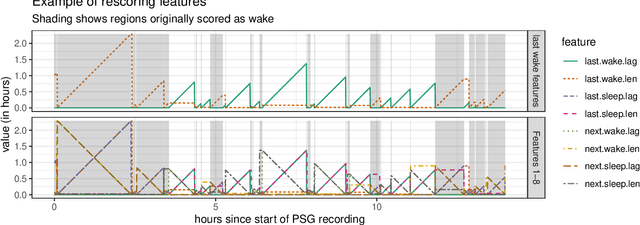
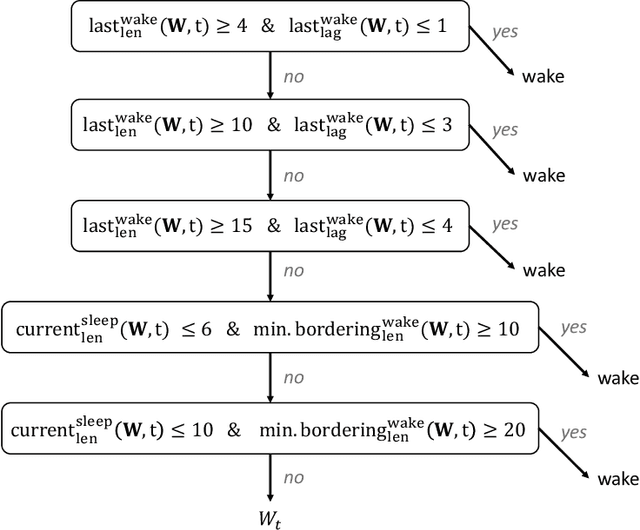
Analyzing temporal data (e.g., wearable device data) requires a decision about how to combine information from the recent and distant past. In the context of classifying sleep status from actigraphy, Webster's rescoring rules offer one popular solution based on the long-term patterns in the output of a moving-window model. Unfortunately, the question of how to optimize rescoring rules for any given setting has remained unsolved. To address this problem and expand the possible use cases of rescoring rules, we propose rephrasing these rules in terms of epoch-specific features. Our features take two general forms: (1) the time lag between now and the most recent [or closest upcoming] bout of time spent in a given state, and (2) the length of the most recent [or closest upcoming] bout of time spent in a given state. Given any initial moving window model, these features can be defined recursively, allowing for straightforward optimization of rescoring rules. Joint optimization of the moving window model and the subsequent rescoring rules can also be implemented using gradient-based optimization software, such as Tensorflow. Beyond binary classification problems (e.g., sleep-wake), the same approach can be applied to summarize long-term patterns for multi-state classification problems (e.g., sitting, walking, or stair climbing). We find that optimized rescoring rules improve the performance of sleep-wake classifiers, achieving accuracy comparable to that of certain neural network architectures.