Online Control of the False Discovery Rate under "Decision Deadlines"
Paper and Code
Oct 15, 2021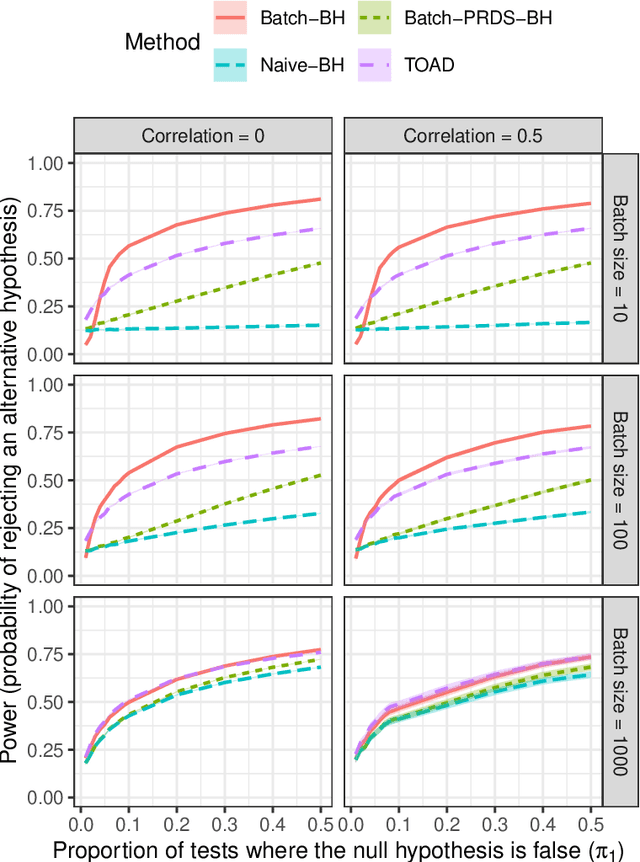

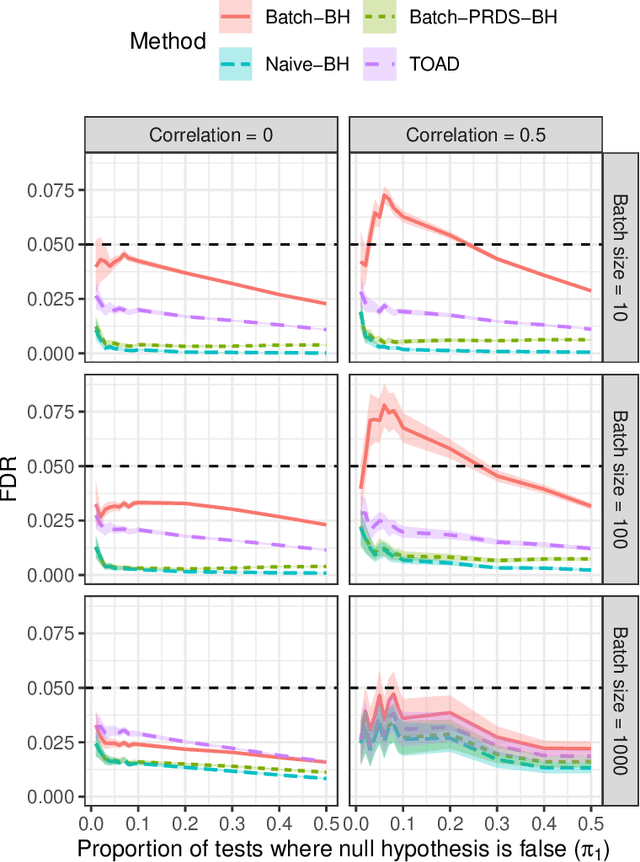
Online testing procedures aim to control the extent of false discoveries over a sequence of hypothesis tests, allowing for the possibility that early-stage test results influence the choice of hypotheses to be tested in later stages. Typically, online methods assume that a permanent decision regarding the current test (reject or not reject) must be made before advancing to the next test. We instead assume that each hypothesis requires an immediate preliminary decision, but also allows us to update that decision until a preset deadline. Roughly speaking, this lets us apply a Benjamini-Hochberg-type procedure over a moving window of hypotheses, where the threshold parameters for upcoming tests can be determined based on preliminary results. Our method controls the false discovery rate (FDR) at every stage of testing, as well as at adaptively chosen stopping times. These results apply even under arbitrary p-value dependency structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge