Support Vector Machines with the Hard-Margin Loss: Optimal Training via Combinatorial Benders' Cuts

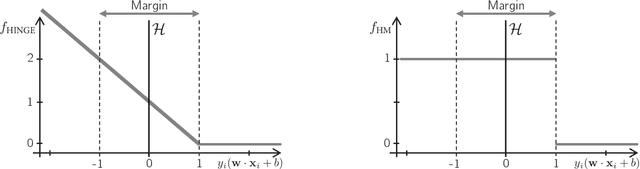
The classical hinge-loss support vector machines (SVMs) model is sensitive to outlier observations due to the unboundedness of its loss function. To circumvent this issue, recent studies have focused on non-convex loss functions, such as the hard-margin loss, which associates a constant penalty to any misclassified or within-margin sample. Applying this loss function yields much-needed robustness for critical applications but it also leads to an NP-hard model that makes training difficult, since current exact optimization algorithms show limited scalability, whereas heuristics are not able to find high-quality solutions consistently. Against this background, we propose new integer programming strategies that significantly improve our ability to train the hard-margin SVM model to global optimality. We introduce an iterative sampling and decomposition approach, in which smaller subproblems are used to separate combinatorial Benders' cuts. Those cuts, used within a branch-and-cut algorithm, permit to converge much more quickly towards a global optimum. Through extensive numerical analyses on classical benchmark data sets, our solution algorithm solves, for the first time, 117 new data sets to optimality and achieves a reduction of 50% in the average optimality gap for the hardest datasets of the benchmark.

PILS: Exploring high-order neighborhoods by pattern mining and injection

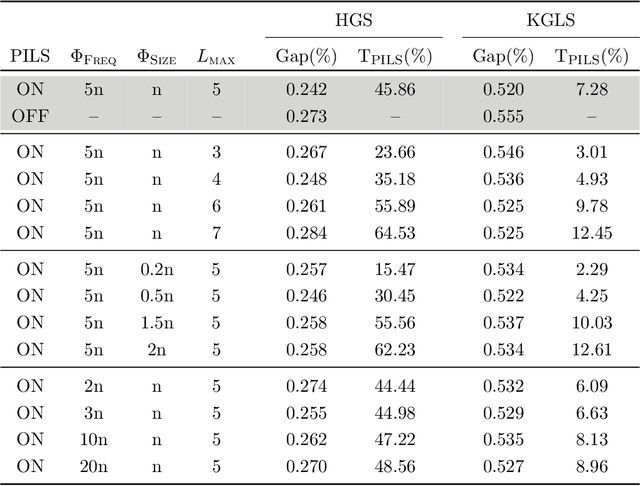
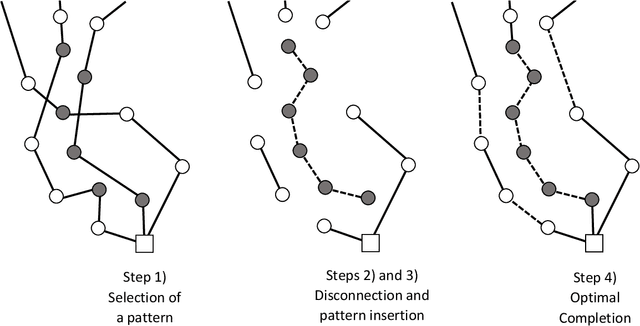
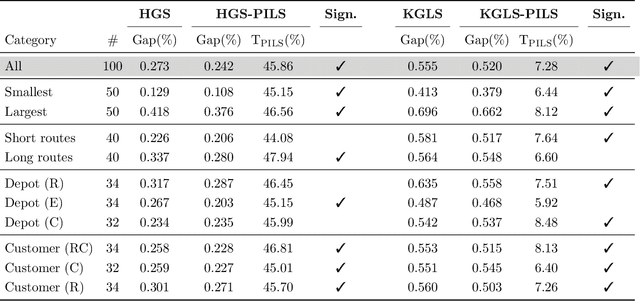
We introduce pattern injection local search (PILS), an optimization strategy that uses pattern mining to explore high-order local-search neighborhoods, and illustrate its application on the vehicle routing problem. PILS operates by storing a limited number of frequent patterns from elite solutions. During the local search, each pattern is used to define one move in which 1) incompatible edges are disconnected, 2) the edges defined by the pattern are reconnected, and 3) the remaining solution fragments are optimally reconnected. Each such move is accepted only in case of solution improvement. As visible in our experiments, this strategy results in a new paradigm of local search, which complements and enhances classical search approaches in a controllable amount of computational time. We demonstrate that PILS identifies useful high-order moves (e.g., 9-opt and 10-opt) which would otherwise not be found by enumeration, and that it significantly improves the performance of state-of-the-art population-based and neighborhood-centered metaheuristics.