ZoPE: A Fast Optimizer for ReLU Networks with Low-Dimensional Inputs
Paper and Code
Jun 09, 2021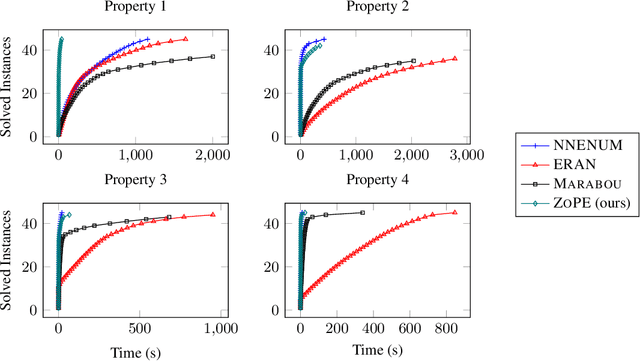


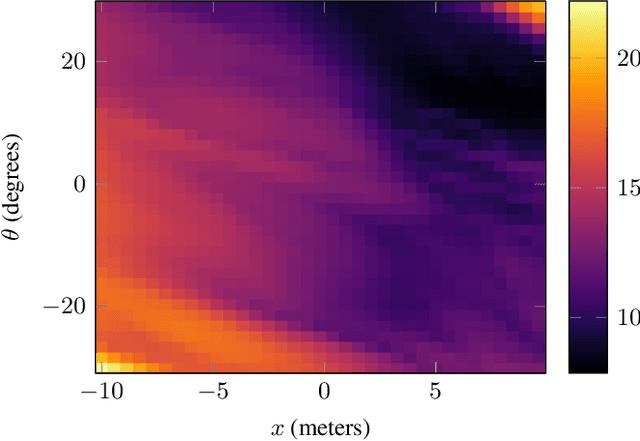
Deep neural networks often lack the safety and robustness guarantees needed to be deployed in safety critical systems. Formal verification techniques can be used to prove input-output safety properties of networks, but when properties are difficult to specify, we rely on the solution to various optimization problems. In this work, we present an algorithm called ZoPE that solves optimization problems over the output of feedforward ReLU networks with low-dimensional inputs. The algorithm eagerly splits the input space, bounding the objective using zonotope propagation at each step, and improves computational efficiency compared to existing mixed integer programming approaches. We demonstrate how to formulate and solve three types of optimization problems: (i) minimization of any convex function over the output space, (ii) minimization of a convex function over the output of two networks in series with an adversarial perturbation in the layer between them, and (iii) maximization of the difference in output between two networks. Using ZoPE, we observe a $25\times$ speedup on property 1 of the ACAS Xu neural network verification benchmark and an $85\times$ speedup on a set of linear optimization problems. We demonstrate the versatility of the optimizer in analyzing networks by projecting onto the range of a generative adversarial network and visualizing the differences between a compressed and uncompressed network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge