ZLPR: A Novel Loss for Multi-label Classification
Paper and Code
Aug 05, 2022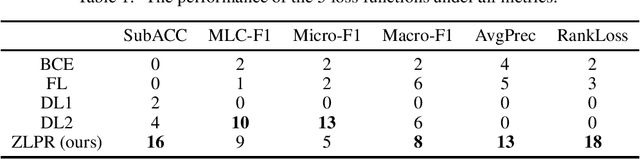
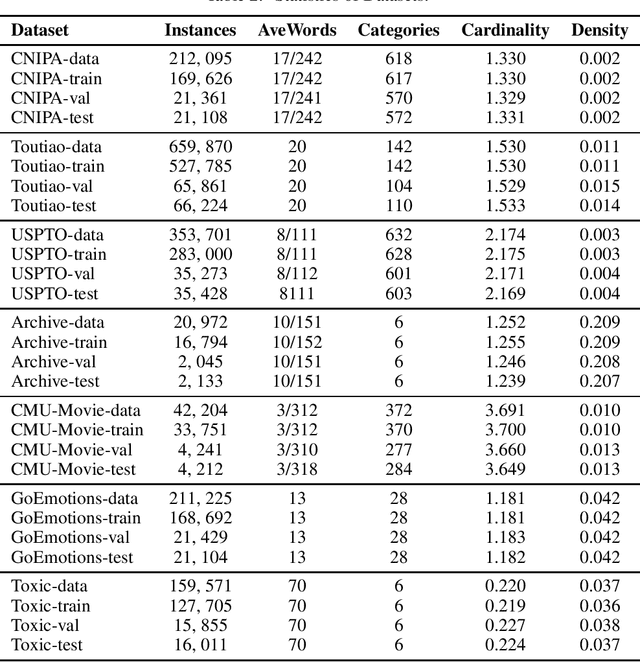
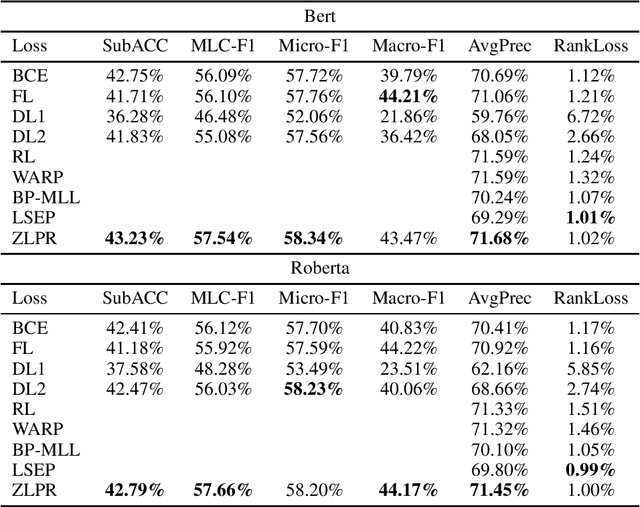
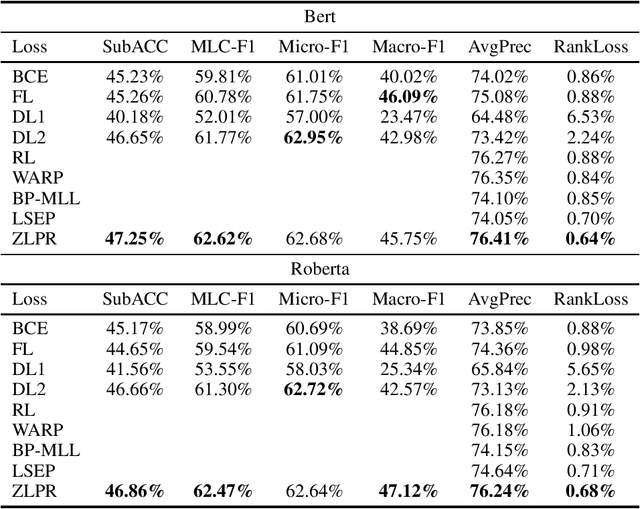
In the era of deep learning, loss functions determine the range of tasks available to models and algorithms. To support the application of deep learning in multi-label classification (MLC) tasks, we propose the ZLPR (zero-bounded log-sum-exp \& pairwise rank-based) loss in this paper. Compared to other rank-based losses for MLC, ZLPR can handel problems that the number of target labels is uncertain, which, in this point of view, makes it equally capable with the other two strategies often used in MLC, namely the binary relevance (BR) and the label powerset (LP). Additionally, ZLPR takes the corelation between labels into consideration, which makes it more comprehensive than the BR methods. In terms of computational complexity, ZLPR can compete with the BR methods because its prediction is also label-independent, which makes it take less time and memory than the LP methods. Our experiments demonstrate the effectiveness of ZLPR on multiple benchmark datasets and multiple evaluation metrics. Moreover, we propose the soft version and the corresponding KL-divergency calculation method of ZLPR, which makes it possible to apply some regularization tricks such as label smoothing to enhance the generalization of models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge