Zeroth-order non-convex learning via hierarchical dual averaging
Paper and Code
Sep 13, 2021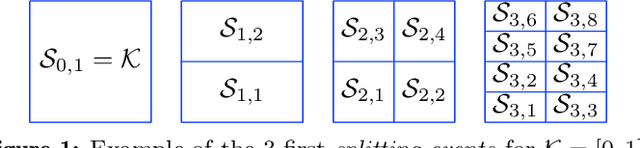
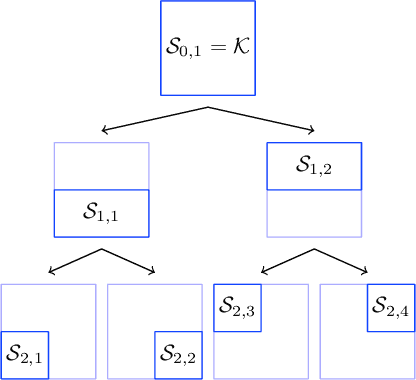
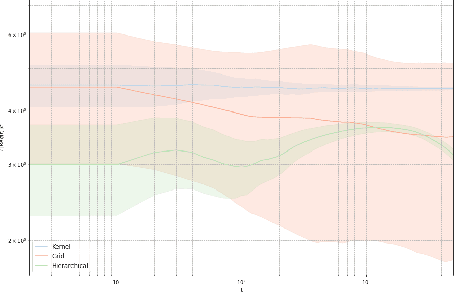
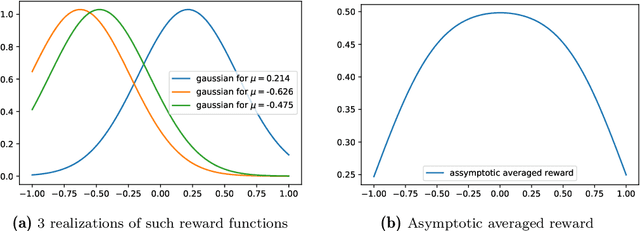
We propose a hierarchical version of dual averaging for zeroth-order online non-convex optimization - i.e., learning processes where, at each stage, the optimizer is facing an unknown non-convex loss function and only receives the incurred loss as feedback. The proposed class of policies relies on the construction of an online model that aggregates loss information as it arrives, and it consists of two principal components: (a) a regularizer adapted to the Fisher information metric (as opposed to the metric norm of the ambient space); and (b) a principled exploration of the problem's state space based on an adapted hierarchical schedule. This construction enables sharper control of the model's bias and variance, and allows us to derive tight bounds for both the learner's static and dynamic regret - i.e., the regret incurred against the best dynamic policy in hindsight over the horizon of play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge