Wide Network Learning with Differential Privacy
Paper and Code
Mar 01, 2021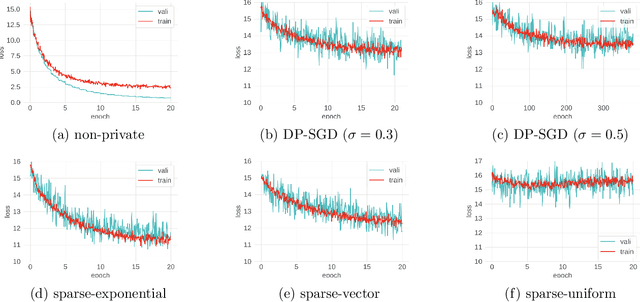
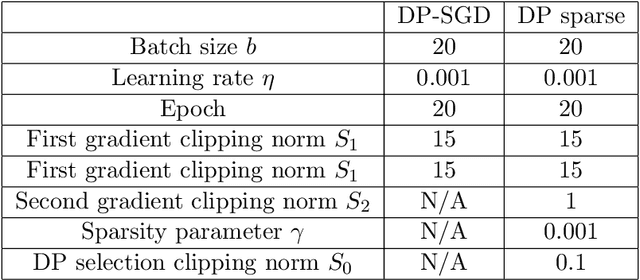
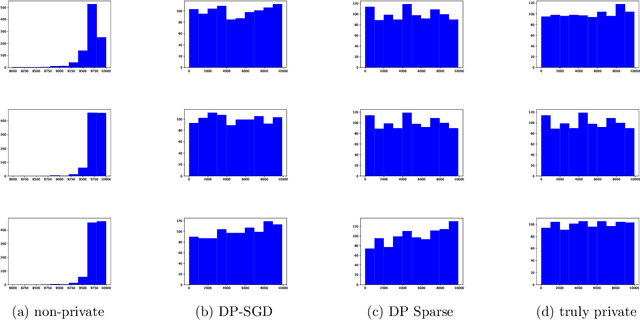
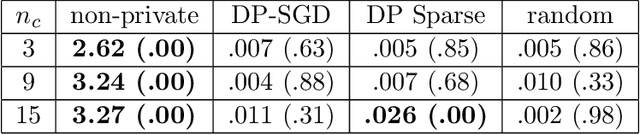
Despite intense interest and considerable effort, the current generation of neural networks suffers a significant loss of accuracy under most practically relevant privacy training regimes. One particularly challenging class of neural networks are the wide ones, such as those deployed for NLP typeahead prediction or recommender systems. Observing that these models share something in common--an embedding layer that reduces the dimensionality of the input--we focus on developing a general approach towards training these models that takes advantage of the sparsity of the gradients. More abstractly, we address the problem of differentially private Empirical Risk Minimization (ERM) for models that admit sparse gradients. We demonstrate that for non-convex ERM problems, the loss is logarithmically dependent on the number of parameters, in contrast with polynomial dependence for the general case. Following the same intuition, we propose a novel algorithm for privately training neural networks. Finally, we provide an empirical study of a DP wide neural network on a real-world dataset, which has been rarely explored in the previous work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge