Why Spectral Normalization Stabilizes GANs: Analysis and Improvements

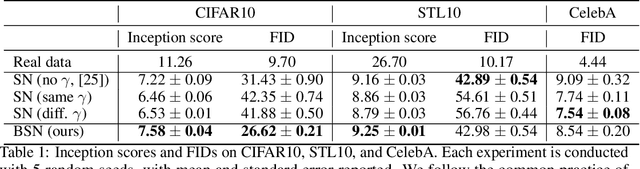
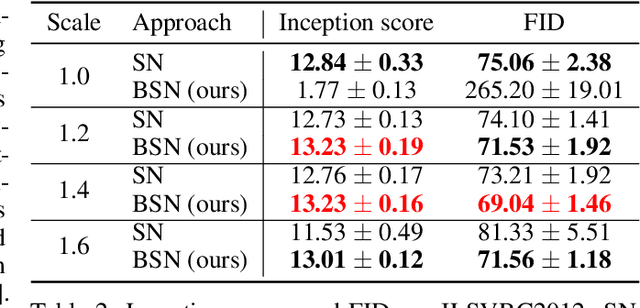
Spectral normalization (SN) is a widely-used technique for improving the stability of Generative Adversarial Networks (GANs) by forcing each layer of the discriminator to have unit spectral norm. This approach controls the Lipschitz constant of the discriminator, and is empirically known to improve sample quality in many GAN architectures. However, there is currently little understanding of why SN is so effective. In this work, we show that SN controls two important failure modes of GAN training: exploding and vanishing gradients. Our proofs illustrate a (perhaps unintentional) connection with the successful LeCun initialization technique, proposed over two decades ago to control gradients in the training of deep neural networks. This connection helps to explain why the most popular implementation of SN for GANs requires no hyperparameter tuning, whereas stricter implementations of SN have poor empirical performance out-of-the-box. Unlike LeCun initialization which only controls gradient vanishing at the beginning of training, we show that SN tends to preserve this property throughout training. Finally, building on this theoretical understanding, we propose Bidirectional Spectral Normalization (BSN), a modification of SN inspired by Xavier initialization, a later improvement to LeCun initialization. Theoretically, we show that BSN gives better gradient control than SN. Empirically, we demonstrate that BSN outperforms SN in sample quality on several benchmark datasets, while also exhibiting better training stability.