Who Leads and Who Follows in Strategic Classification?
Paper and Code
Jun 23, 2021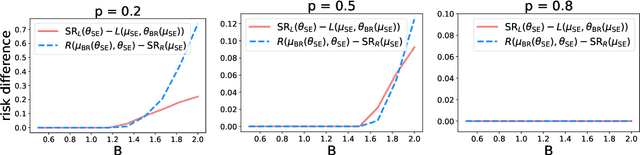


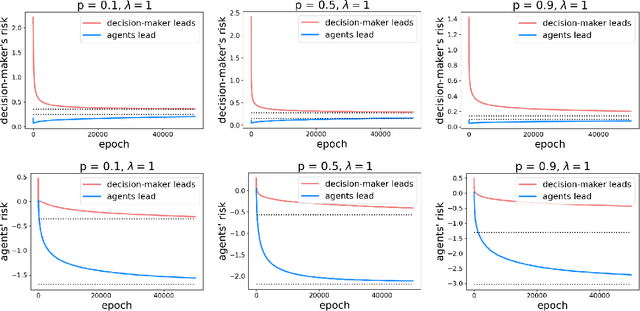
As predictive models are deployed into the real world, they must increasingly contend with strategic behavior. A growing body of work on strategic classification treats this problem as a Stackelberg game: the decision-maker "leads" in the game by deploying a model, and the strategic agents "follow" by playing their best response to the deployed model. Importantly, in this framing, the burden of learning is placed solely on the decision-maker, while the agents' best responses are implicitly treated as instantaneous. In this work, we argue that the order of play in strategic classification is fundamentally determined by the relative frequencies at which the decision-maker and the agents adapt to each other's actions. In particular, by generalizing the standard model to allow both players to learn over time, we show that a decision-maker that makes updates faster than the agents can reverse the order of play, meaning that the agents lead and the decision-maker follows. We observe in standard learning settings that such a role reversal can be desirable for both the decision-maker and the strategic agents. Finally, we show that a decision-maker with the freedom to choose their update frequency can induce learning dynamics that converge to Stackelberg equilibria with either order of play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge