Who is in Your Top Three? Optimizing Learning in Elections with Many Candidates
Paper and Code
Jun 19, 2019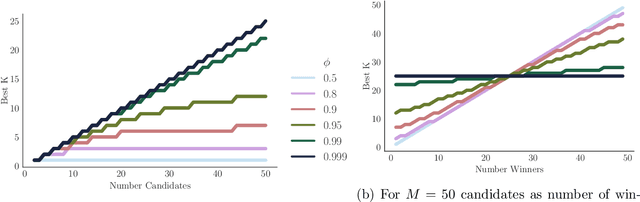
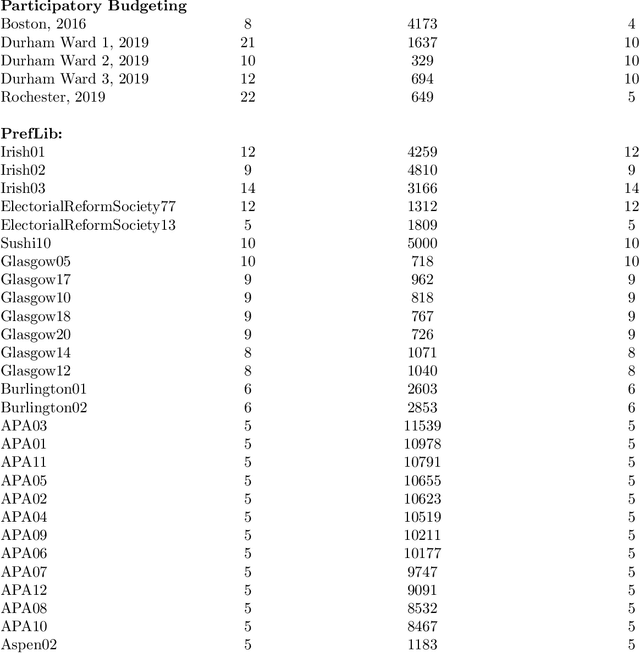
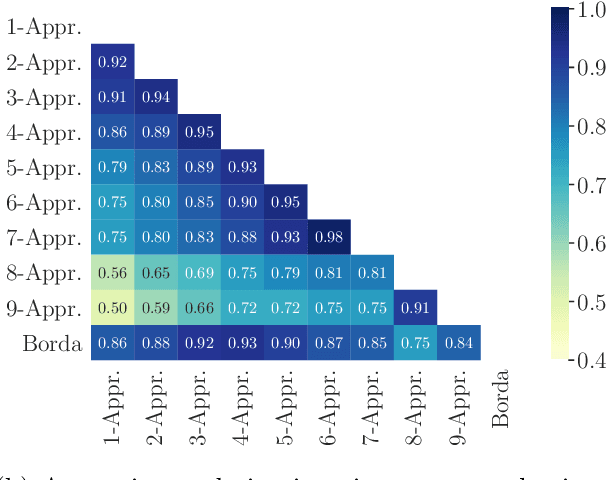
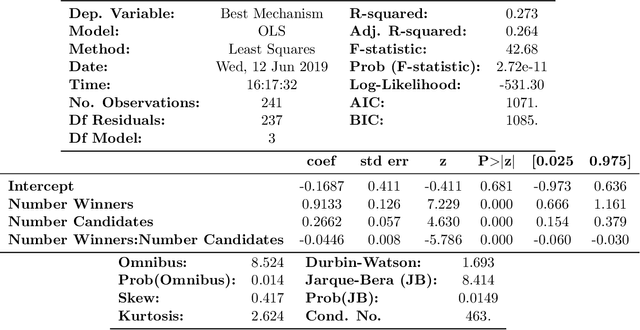
Elections and opinion polls often have many candidates, with the aim to either rank the candidates or identify a small set of winners according to voters' preferences. In practice, voters do not provide a full ranking; instead, each voter provides their favorite K candidates, potentially in ranked order. The election organizer must choose K and an aggregation rule. We provide a theoretical framework to make these choices. Each K-Approval or K-partial ranking mechanism (with a corresponding positional scoring rule) induces a learning rate for the speed at which the election correctly recovers the asymptotic outcome. Given the voter choice distribution, the election planner can thus identify the rate optimal mechanism. Earlier work in this area provides coarse order-of-magnitude guaranties which are not sufficient to make such choices. Our framework further resolves questions of when randomizing between multiple mechanisms may improve learning, for arbitrary voter noise models. Finally, we use data from 5 large participatory budgeting elections that we organized across several US cities, along with other ranking data, to demonstrate the utility of our methods. In particular, we find that historically such elections have set K too low and that picking the right mechanism can be the difference between identifying the ultimate winner with only a 80% probability or a 99.9% probability after 400 voters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge