When to Localize? A POMDP Approach
Paper and Code
Nov 13, 2024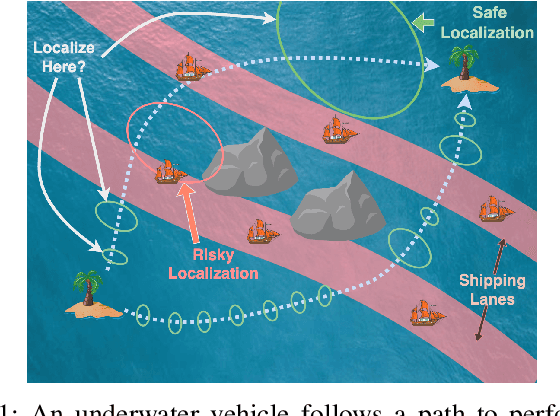
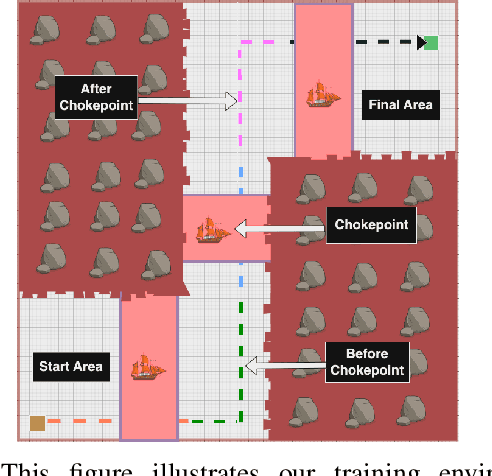
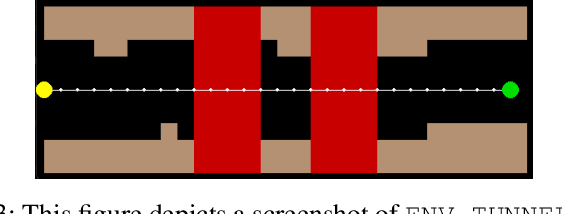
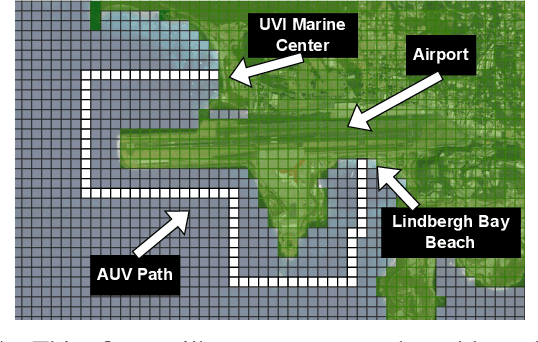
Robots often localize to lower navigational errors and facilitate downstream, high-level tasks. However, a robot may want to selectively localize when localization is costly (such as with resource-constrained robots) or inefficient (for example, submersibles that need to surface), especially when navigating in environments with variable numbers of hazards such as obstacles and shipping lanes. In this study, we propose a method that helps a robot determine ``when to localize'' to 1) minimize such actions and 2) not exceed the probability of failure (such as surfacing within high-traffic shipping lanes). We formulate our method as a Constrained Partially Observable Markov Decision Process and use the Cost-Constrained POMCP solver to plan the robot's actions. The solver simulates failure probabilities to decide if a robot moves to its goal or localizes to prevent failure. We performed numerical experiments with multiple baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge