Weighted QMIX: Expanding Monotonic Value Function Factorisation

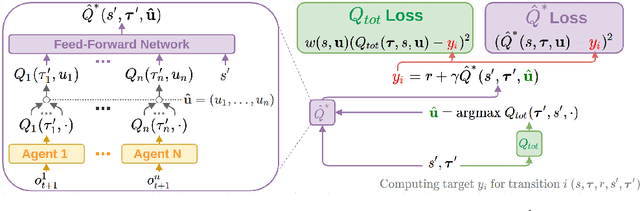
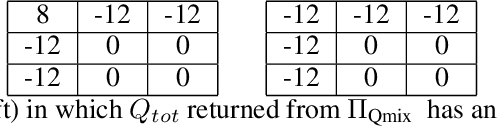
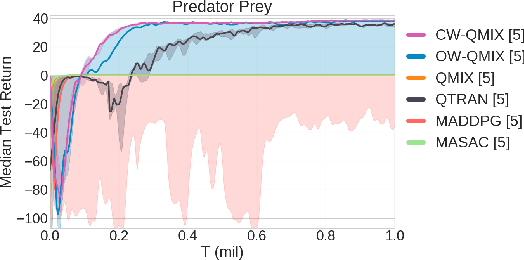
QMIX is a popular $Q$-learning algorithm for cooperative MARL in the centralised training and decentralised execution paradigm. In order to enable easy decentralisation, QMIX restricts the joint action $Q$-values it can represent to be a monotonic mixing of each agent's utilities. However, this restriction prevents it from representing value functions in which an agent's ordering over its actions can depend on other agents' actions. To analyse this representational limitation, we first formalise the objective QMIX optimises, which allows us to view QMIX as an operator that first computes the $Q$-learning targets and then projects them into the space representable by QMIX. This projection returns a representable $Q$-value that minimises the unweighted squared error across all joint actions. We show in particular that this projection can fail to recover the optimal policy even with access to $Q^*$, which primarily stems from the equal weighting placed on each joint action. We rectify this by introducing a weighting into the projection, in order to place more importance on the better joint actions. We propose two weighting schemes and prove that they recover the correct maximal action for any joint action $Q$-values, and therefore for $Q^*$ as well. Based on our analysis and results in the tabular setting we introduce two scalable versions of our algorithm, Centrally-Weighted (CW) QMIX and Optimistically-Weighted (OW) QMIX and demonstrate improved performance on both predator-prey and challenging multi-agent StarCraft benchmark tasks.