Voted Kernel Regularization
Paper and Code
Sep 14, 2015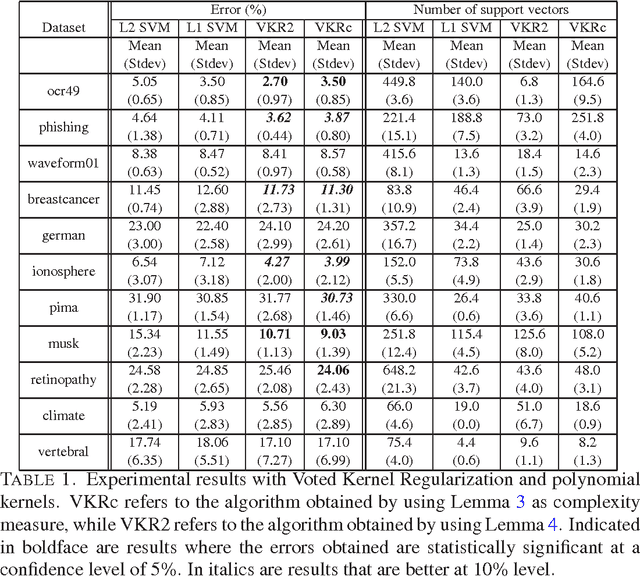
This paper presents an algorithm, Voted Kernel Regularization , that provides the flexibility of using potentially very complex kernel functions such as predictors based on much higher-degree polynomial kernels, while benefitting from strong learning guarantees. The success of our algorithm arises from derived bounds that suggest a new regularization penalty in terms of the Rademacher complexities of the corresponding families of kernel maps. In a series of experiments we demonstrate the improved performance of our algorithm as compared to baselines. Furthermore, the algorithm enjoys several favorable properties. The optimization problem is convex, it allows for learning with non-PDS kernels, and the solutions are highly sparse, resulting in improved classification speed and memory requirements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge