von Mises-Fisher Mixture Model-based Deep learning: Application to Face Verification
Paper and Code
Dec 31, 2017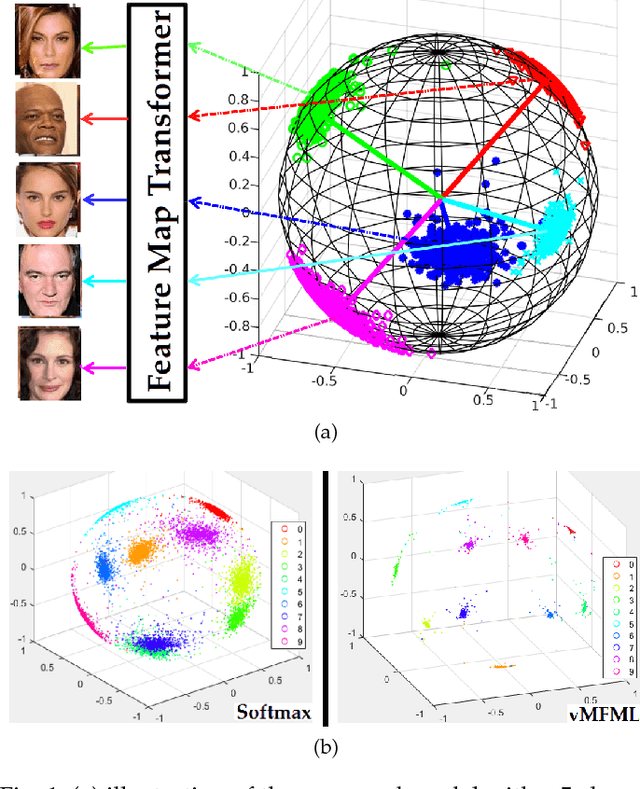
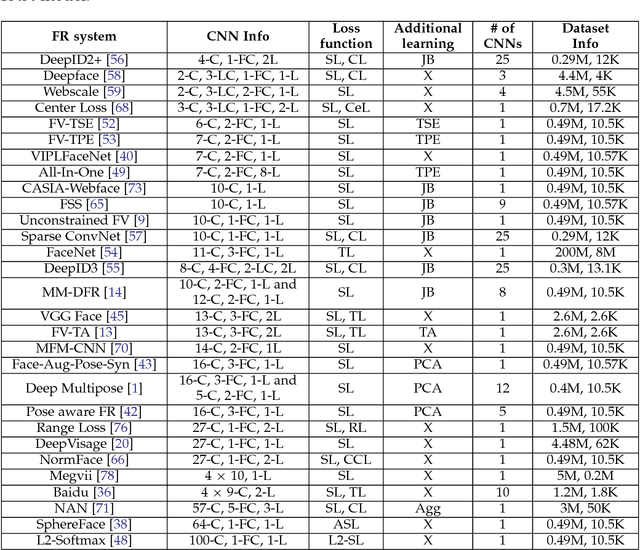
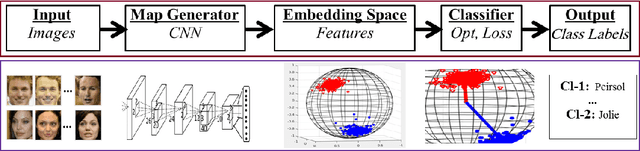
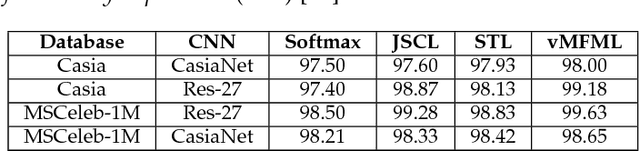
A number of pattern recognition tasks, \textit{e.g.}, face verification, can be boiled down to classification or clustering of unit length directional feature vectors whose distance can be simply computed by their angle. In this paper, we propose the von Mises-Fisher (vMF) mixture model as the theoretical foundation for an effective deep-learning of such directional features and derive a novel vMF Mixture Loss and its corresponding vMF deep features. The proposed vMF feature learning achieves the characteristics of discriminative learning, \textit{i.e.}, compacting the instances of the same class while increasing the distance of instances from different classes. Moreover, it subsumes a number of popular loss functions as well as an effective method in deep learning, namely normalization. We conduct extensive experiments on face verification using 4 different challenging face datasets, \textit{i.e.}, LFW, YouTube faces, CACD and IJB-A. Results show the effectiveness and excellent generalization ability of the proposed approach as it achieves state-of-the-art results on the LFW, YouTube faces and CACD datasets and competitive results on the IJB-A dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge