VISA: Variational Inference with Sequential Sample-Average Approximations
Paper and Code
Mar 15, 2024
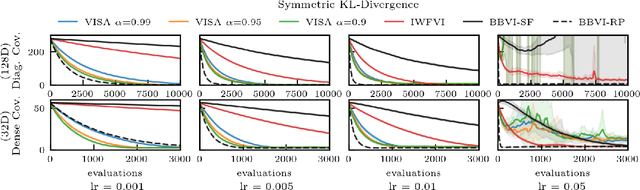
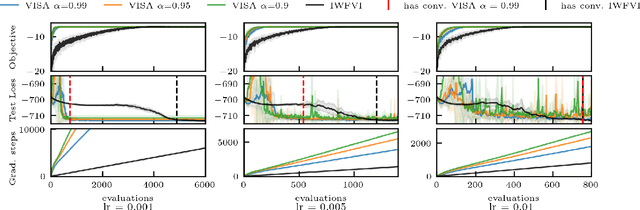
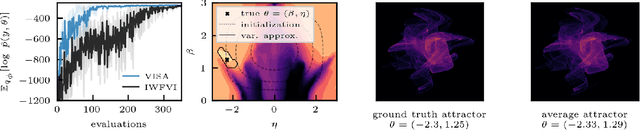
We present variational inference with sequential sample-average approximation (VISA), a method for approximate inference in computationally intensive models, such as those based on numerical simulations. VISA extends importance-weighted forward-KL variational inference by employing a sequence of sample-average approximations, which are considered valid inside a trust region. This makes it possible to reuse model evaluations across multiple gradient steps, thereby reducing computational cost. We perform experiments on high-dimensional Gaussians, Lotka-Volterra dynamics, and a Pickover attractor, which demonstrate that VISA can achieve comparable approximation accuracy to standard importance-weighted forward-KL variational inference with computational savings of a factor two or more for conservatively chosen learning rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge