VFunc: a Deep Generative Model for Functions
Paper and Code
Jul 11, 2018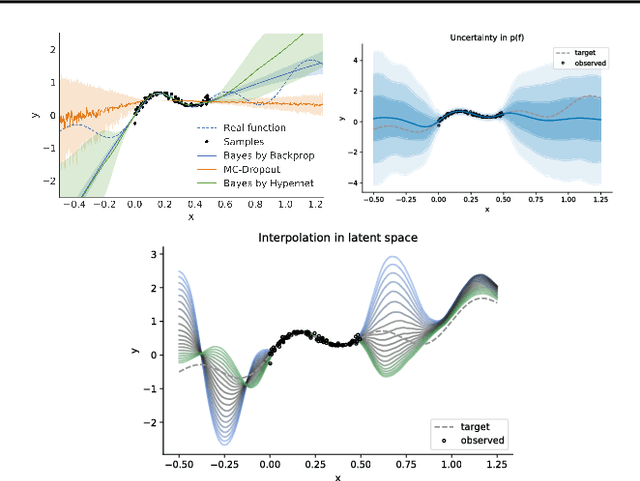

We introduce a deep generative model for functions. Our model provides a joint distribution p(f, z) over functions f and latent variables z which lets us efficiently sample from the marginal p(f) and maximize a variational lower bound on the entropy H(f). We can thus maximize objectives of the form E_{f~p(f)}[R(f)] + c*H(f), where R(f) denotes, e.g., a data log-likelihood term or an expected reward. Such objectives encompass Bayesian deep learning in function space, rather than parameter space, and Bayesian deep RL with representations of uncertainty that offer benefits over bootstrapping and parameter noise. In this short paper we describe our model, situate it in the context of prior work, and present proof-of-concept experiments for regression and RL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge