Vertex Nomination, Consistent Estimation, and Adversarial Modification

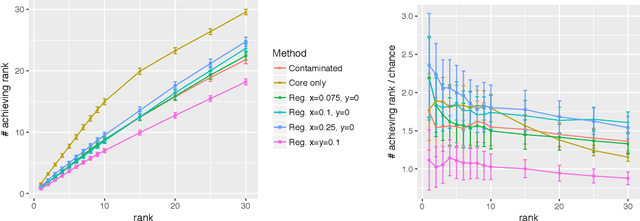
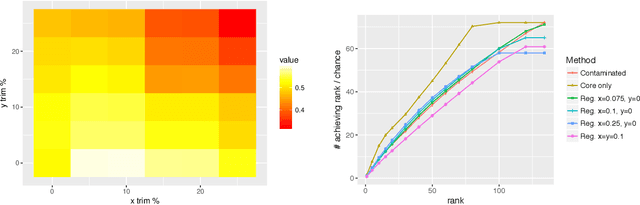
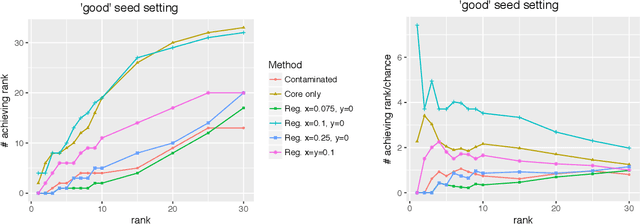
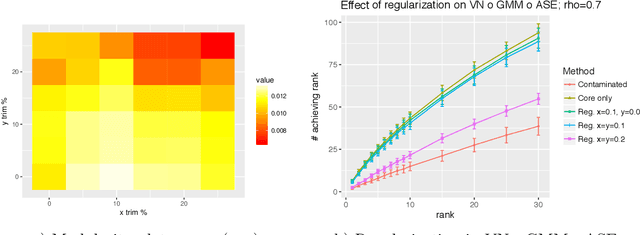
Given a pair of graphs $G_1$ and $G_2$ and a vertex set of interest in $G_1$, the vertex nomination problem seeks to find the corresponding vertices of interest in $G_2$ (if they exist) and produce a rank list of the vertices in $G_2$, with the corresponding vertices of interest in $G_2$ concentrating, ideally, at the top of the rank list. In this paper we study the effect of an adversarial contamination model on the performance of a spectral graph embedding-based vertex nomination scheme. In both real and simulated examples, we demonstrate that this vertex nomination scheme performs effectively in the uncontaminated setting; adversarial network contamination adversely impacts the performance of our VN scheme; and network regularization successfully mitigates the impact of the contamination. In addition to furthering the theoretic basis of consistency in vertex nomination, the adversarial noise model posited herein is grounded in theoretical developments that allow us to frame the role of an adversary in terms of maximal vertex nomination consistency classes.