Versatile Neural Processes for Learning Implicit Neural Representations

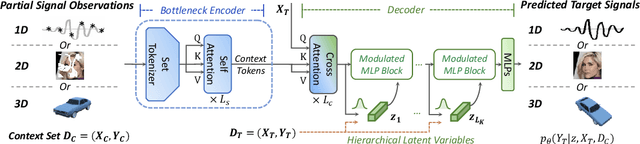
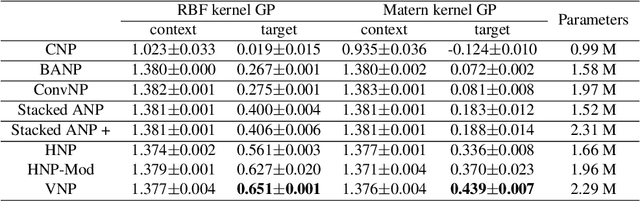
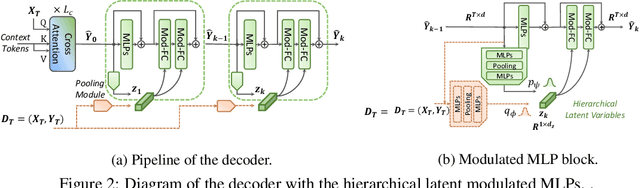
Representing a signal as a continuous function parameterized by neural network (a.k.a. Implicit Neural Representations, INRs) has attracted increasing attention in recent years. Neural Processes (NPs), which model the distributions over functions conditioned on partial observations (context set), provide a practical solution for fast inference of continuous functions. However, existing NP architectures suffer from inferior modeling capability for complex signals. In this paper, we propose an efficient NP framework dubbed Versatile Neural Processes (VNP), which largely increases the capability of approximating functions. Specifically, we introduce a bottleneck encoder that produces fewer and informative context tokens, relieving the high computational cost while providing high modeling capability. At the decoder side, we hierarchically learn multiple global latent variables that jointly model the global structure and the uncertainty of a function, enabling our model to capture the distribution of complex signals. We demonstrate the effectiveness of the proposed VNP on a variety of tasks involving 1D, 2D and 3D signals. Particularly, our method shows promise in learning accurate INRs w.r.t. a 3D scene without further finetuning.