Vehicle Re-identification Based on Dual Distance Center Loss

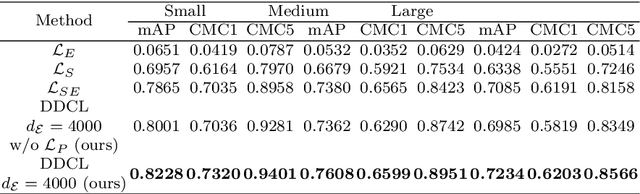
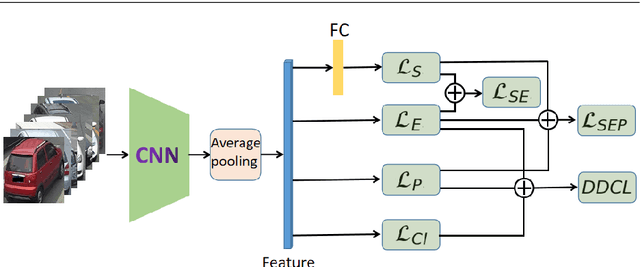
Recently, deep learning has been widely used in the field of vehicle re-identification. When training a deep model, softmax loss is usually used as a supervision tool. However, the softmax loss performs well for closed-set tasks, but not very well for open-set tasks. In this paper, we sum up five shortcomings of center loss and solved all of them by proposing a dual distance center loss (DDCL). Especially we solve the shortcoming that center loss must combine with the softmax loss to supervise training the model, which provides us with a new perspective to examine the center loss. In addition, we verify the inconsistency between the proposed DDCL and softmax loss in the feature space, which makes the center loss no longer be limited by the softmax loss in the feature space after removing the softmax loss. To be specifically, we add the Pearson distance on the basis of the Euclidean distance to the same center, which makes all features of the same class be confined to the intersection of a hypersphere and a hypercube in the feature space. The proposed Pearson distance strengthens the intra-class compactness of the center loss and enhances the generalization ability of center loss. Moreover, by designing a Euclidean distance threshold between all center pairs, which not only strengthens the inter-class separability of center loss, but also makes the center loss (or DDCL) works well without the combination of softmax loss. We apply DDCL in the field of vehicle re-identification named VeRi-776 dataset and VehicleID dataset. And in order to verify its good generalization ability, we also verify it in two datasets commonly used in the field of person re-identification named MSMT17 dataset and Market1501 dataset.