VectorAdam for Rotation Equivariant Geometry Optimization

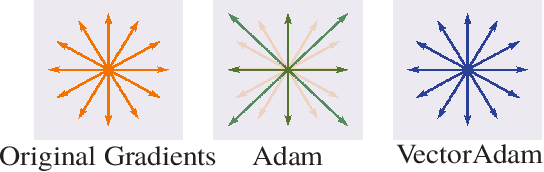
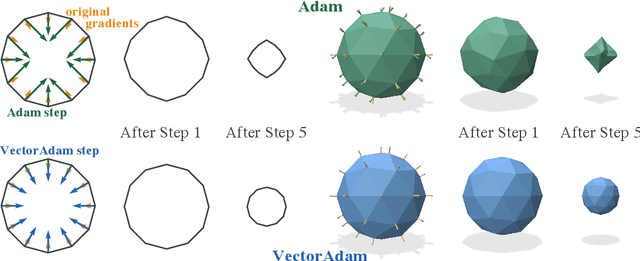
The rise of geometric problems in machine learning has necessitated the development of equivariant methods, which preserve their output under the action of rotation or some other transformation. At the same time, the Adam optimization algorithm has proven remarkably effective across machine learning and even traditional tasks in geometric optimization. In this work, we observe that naively applying Adam to optimize vector-valued data is not rotation equivariant, due to per-coordinate moment updates, and in fact this leads to significant artifacts and biases in practice. We propose to resolve this deficiency with VectorAdam, a simple modification which makes Adam rotation-equivariant by accounting for the vector structure of optimization variables. We demonstrate this approach on problems in machine learning and traditional geometric optimization, showing that equivariant VectorAdam resolves the artifacts and biases of traditional Adam when applied to vector-valued data, with equivalent or even improved rates of convergence.