Variation-Incentive Loss Re-weighting for Regression Analysis on Biased Data
Paper and Code
Sep 14, 2021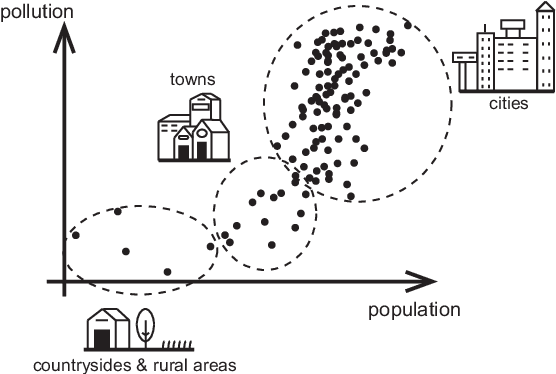
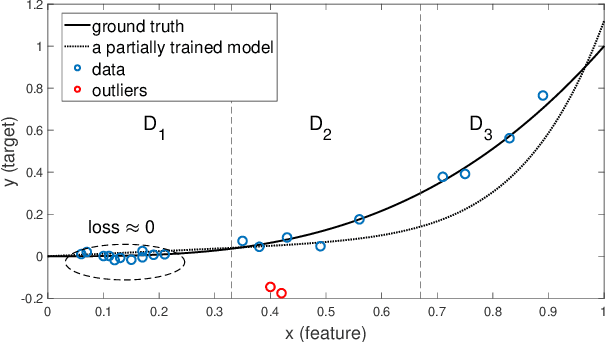
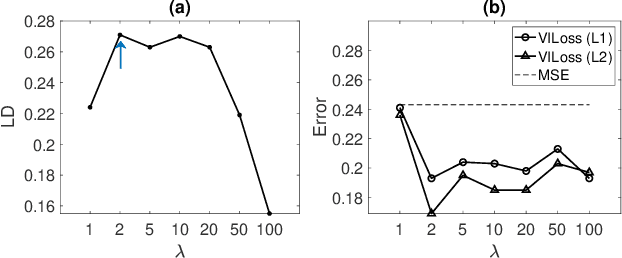
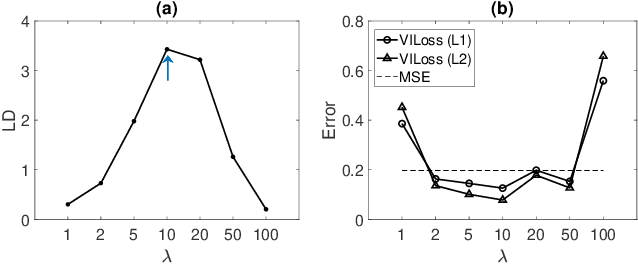
Both classification and regression tasks are susceptible to the biased distribution of training data. However, existing approaches are focused on the class-imbalanced learning and cannot be applied to the problems of numerical regression where the learning targets are continuous values rather than discrete labels. In this paper, we aim to improve the accuracy of the regression analysis by addressing the data skewness/bias during model training. We first introduce two metrics, uniqueness and abnormality, to reflect the localized data distribution from the perspectives of their feature (i.e., input) space and target (i.e., output) space. Combining these two metrics we propose a Variation-Incentive Loss re-weighting method (VILoss) to optimize the gradient descent-based model training for regression analysis. We have conducted comprehensive experiments on both synthetic and real-world data sets. The results show significant improvement in the model quality (reduction in error by up to 11.9%) when using VILoss as the loss criterion in training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge