Variants of Tagged Sentential Decision Diagrams
Paper and Code
Nov 16, 2023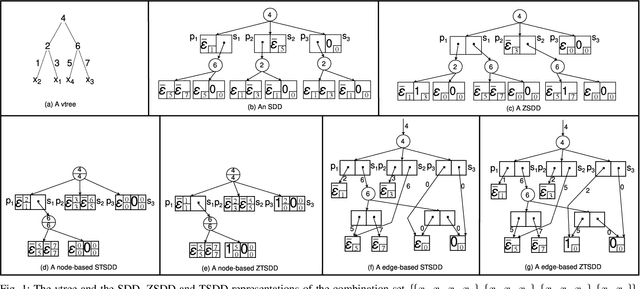

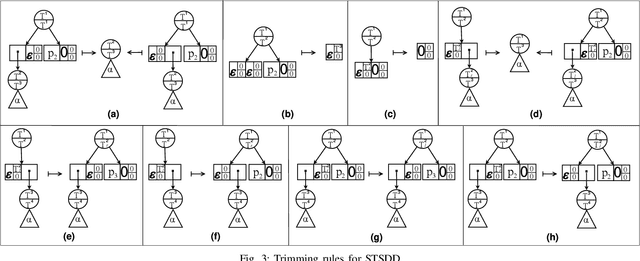
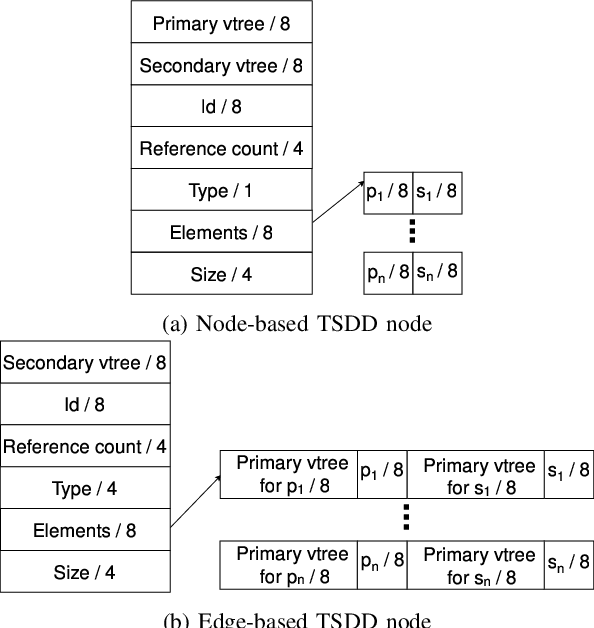
A recently proposed canonical form of Boolean functions, namely tagged sentential decision diagrams (TSDDs), exploits both the standard and zero-suppressed trimming rules. The standard ones minimize the size of sentential decision diagrams (SDDs) while the zero-suppressed trimming rules have the same objective as the standard ones but for zero-suppressed sentential decision diagrams (ZSDDs). The original TSDDs, which we call zero-suppressed TSDDs (ZTSDDs), firstly fully utilize the zero-suppressed trimming rules, and then the standard ones. In this paper, we present a variant of TSDDs which we call standard TSDDs (STSDDs) by reversing the order of trimming rules. We then prove the canonicity of STSDDs and present the algorithms for binary operations on TSDDs. In addition, we offer two kinds of implementations of STSDDs and ZTSDDs and acquire three variations of the original TSDDs. Experimental evaluations demonstrate that the four versions of TSDDs have the size advantage over SDDs and ZSDDs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge