Variance Reduction with Sparse Gradients
Paper and Code
Jan 27, 2020
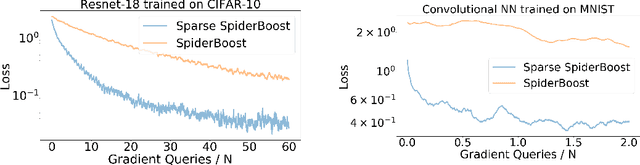
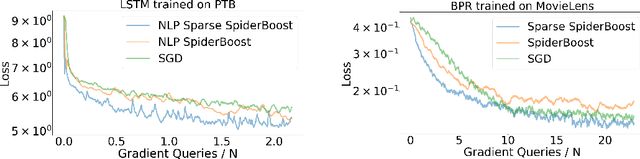
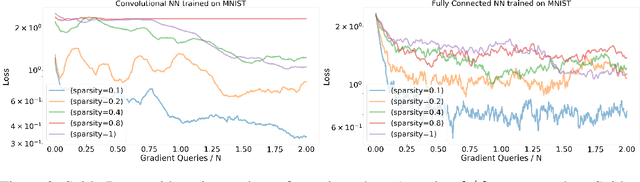
Variance reduction methods such as SVRG and SpiderBoost use a mixture of large and small batch gradients to reduce the variance of stochastic gradients. Compared to SGD, these methods require at least double the number of operations per update to model parameters. To reduce the computational cost of these methods, we introduce a new sparsity operator: The random-top-k operator. Our operator reduces computational complexity by estimating gradient sparsity exhibited in a variety of applications by combining the top-k operator and the randomized coordinate descent operator. With this operator, large batch gradients offer an extra benefit beyond variance reduction: A reliable estimate of gradient sparsity. Theoretically, our algorithm is at least as good as the best algorithm (SpiderBoost), and further excels in performance whenever the random-top-k operator captures gradient sparsity. Empirically, our algorithm consistently outperforms SpiderBoost using various models on various tasks including image classification, natural language processing, and sparse matrix factorization. We also provide empirical evidence to support the intuition behind our algorithm via a simple gradient entropy computation, which serves to quantify gradient sparsity at every iteration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge