Using Neural Networks to Compute Approximate and Guaranteed Feasible Hamilton-Jacobi-Bellman PDE Solutions
Paper and Code
Mar 27, 2017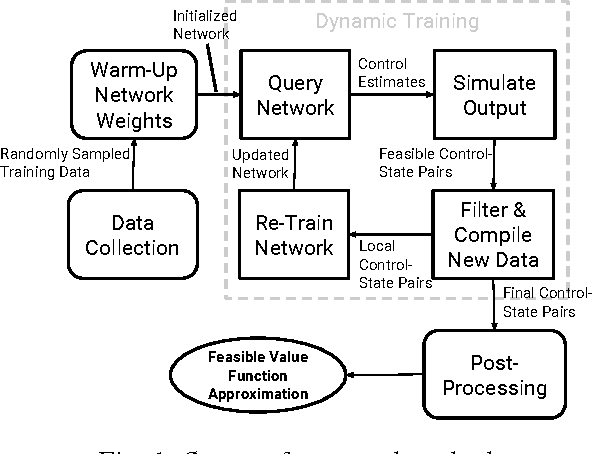
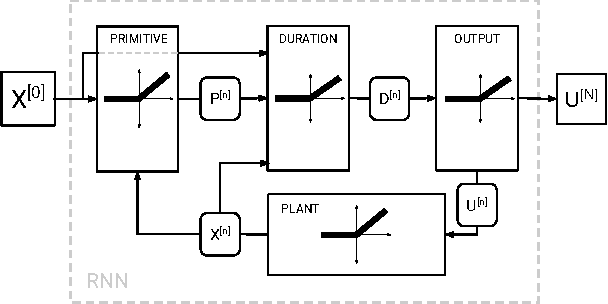
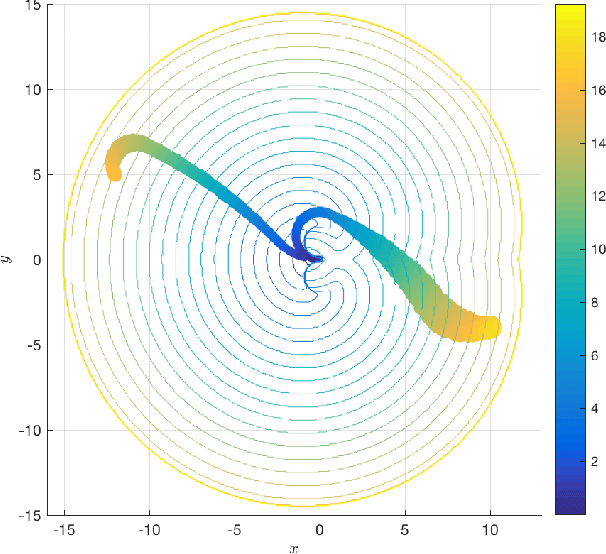
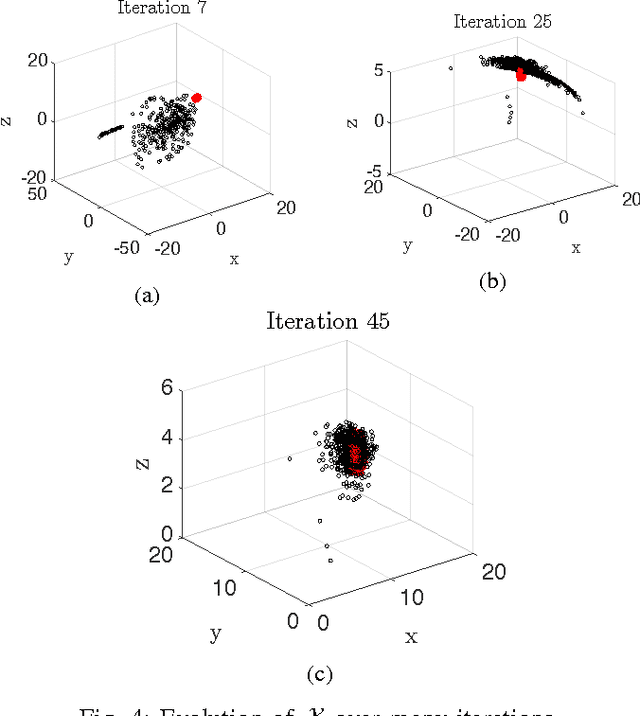
To sidestep the curse of dimensionality when computing solutions to Hamilton-Jacobi-Bellman partial differential equations (HJB PDE), we propose an algorithm that leverages a neural network to approximate the value function. We show that our final approximation of the value function generates near optimal controls which are guaranteed to successfully drive the system to a target state. Our framework is not dependent on state space discretization, leading to a significant reduction in computation time and space complexity in comparison with dynamic programming-based approaches. Using this grid-free approach also enables us to plan over longer time horizons with relatively little additional computation overhead. Unlike many previous neural network HJB PDE approximating formulations, our approximation is strictly conservative and hence any trajectories we generate will be strictly feasible. For demonstration, we specialize our new general framework to the Dubins car model and discuss how the framework can be applied to other models with higher-dimensional state spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge