Using Centroidal Voronoi Tessellations to Scale Up the Multi-dimensional Archive of Phenotypic Elites Algorithm
Paper and Code
Jul 29, 2017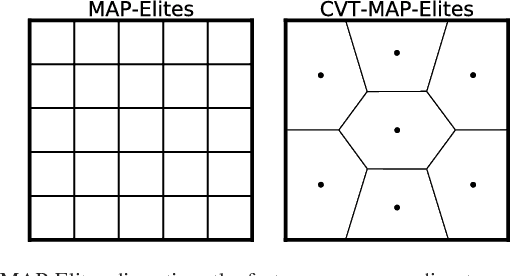
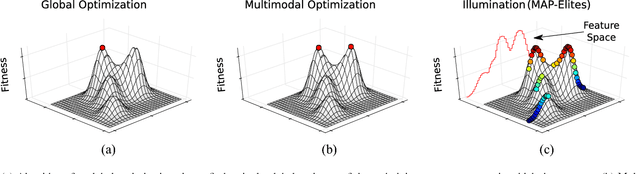
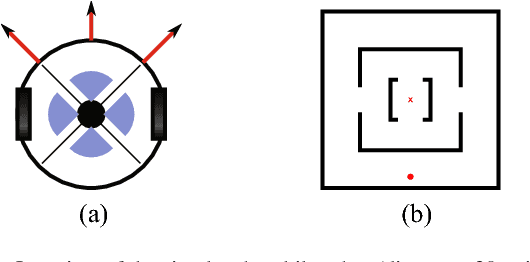

The recently introduced Multi-dimensional Archive of Phenotypic Elites (MAP-Elites) is an evolutionary algorithm capable of producing a large archive of diverse, high-performing solutions in a single run. It works by discretizing a continuous feature space into unique regions according to the desired discretization per dimension. While simple, this algorithm has a main drawback: it cannot scale to high-dimensional feature spaces since the number of regions increase exponentially with the number of dimensions. In this paper, we address this limitation by introducing a simple extension of MAP-Elites that has a constant, pre-defined number of regions irrespective of the dimensionality of the feature space. Our main insight is that methods from computational geometry could partition a high-dimensional space into well-spread geometric regions. In particular, our algorithm uses a centroidal Voronoi tessellation (CVT) to divide the feature space into a desired number of regions; it then places every generated individual in its closest region, replacing a less fit one if the region is already occupied. We demonstrate the effectiveness of the new "CVT-MAP-Elites" algorithm in high-dimensional feature spaces through comparisons against MAP-Elites in maze navigation and hexapod locomotion tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge